解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
对互质的正整数 $a, b$, 用 $\left(a^{-1} \bmod b\right)$ 表示满足 $a m \equiv 1(\bmod b)$ 且 $0 \leq m < $ $b$ 的唯一整数 $m$.
(1) 求证: 对任意两两互质的正整数 $a, b, c, 1 < a < b < c$, 都有
$$
\left(a^{-1} \bmod b\right)+\left(b^{-1} \bmod c\right)+\left(c^{-1} \bmod a\right)>\sqrt{a} .
$$
(2) 求证: 对任意正整数 $M$, 存在两两互质的正整数 $a, b, c$, 满足 $M < a < b < $ $c$, 且
$$
\left(a^{-1} \bmod b\right)+\left(b^{-1} \bmod c\right)+\left(c^{-1} \bmod a\right) < 100 \sqrt{a} .
$$
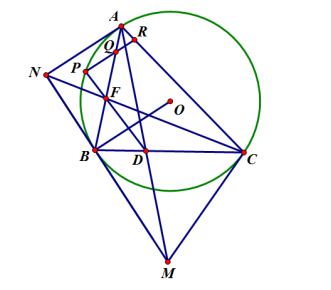
如图, 在锐角 $\triangle A B C$ 中, $\Omega$ 是外接圆, $O$ 是外心, $\Omega$ 在 $B, C$ 处的切线交于点 $M$, 在 $A, B$ 处的切线交于点 $N$. 设 $A M$ 交 $B C$ 于点 $D, C N$ 交 $A B$ 于点 $F$, 延长 $D F$ 交 $\Omega$ 于点 $P$. 过 $P$ 作 $B O$ 的平行线交线段 $A B, A C$ 分别于点 $Q, R$.若 $P Q^2=P R \cdot Q R$, 求 $\angle A C B$ 的值.
将每个正整数染为 $c_1, c_2, c_3, c_4$ 四种颜色之一.
(1) 求证: 存在正整数 $n$ 以及 $i, j \in\{1,2,3,4\}$, 使得 $n$ 的全体正约数中 $c_i$ 颜色的数比 $c_j$ 颜色的数至少多 3 个;
(2) 求证: 对任意正整数 $A$, 存在正整数 $n$ 以及 $i, j \in\{1,2,3,4\}$, 使得 $n$ 的全体正约数中 $c_i$ 颜色的数比 $c_j$ 颜色的数至少多 $A$ 个.