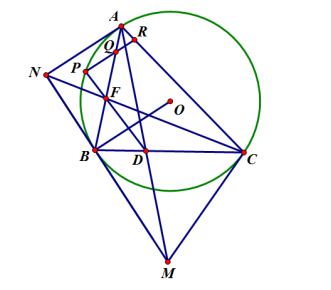
如图, 在锐角 $\triangle A B C$ 中, $\Omega$ 是外接圆, $O$ 是外心, $\Omega$ 在 $B, C$ 处的切线交于点 $M$, 在 $A, B$ 处的切线交于点 $N$. 设 $A M$ 交 $B C$ 于点 $D, C N$ 交 $A B$ 于点 $F$, 延长 $D F$ 交 $\Omega$ 于点 $P$. 过 $P$ 作 $B O$ 的平行线交线段 $A B, A C$ 分别于点 $Q, R$.若 $P Q^2=P R \cdot Q R$, 求 $\angle A C B$ 的值.