解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图1. 已知四边形 $A B C D$ 是矩形. 点 $\mathrm{E}$在 $B A$ 的延长线上. $A E=A D . E C$ 与 $B D$ 相交于点 $G$, 与 $A D$相交于点 $F, A F=A B$.
(1) 求证: $B D \perp E C$;
(2) 若 $A B=1$, 求 $A E$ 的长;

(3)如图2, 连接 $A G$, 求证: $E G-D G=\sqrt{ 2} A G$.

在 $\triangle A B C$ 中, $\angle C=90^{\circ}, A C>B C$, $D$ 是 $A B$ 的中点. $E$ 为直线上一动点, 连接 $D E$, 过点 $D$ 作 $\mathrm{DF} \perp \mathrm{DE}$, 交直线 $B C$ 于点 $F$, 连接 $\mathrm{FF}$.
(1)如图1, 当 $\mathrm{E}$ 是线段 $\mathrm{AC}$ 的中点时, 设 $A E=a, B F=b$,求EF的长 (用含 $a, b$ 的式子表示);
(2)当点 $\mathrm{E}$ 在线段 $C A$ 的延长线上时, 依题意补全图2, 用等式表示线段 $A E, E F, B F$ 之间的数量关系, 并证明.

如图, $\triangle A D E$ 由 $\triangle A B C$ 绕点 $A$ 按逆时针方向旋转 $90^{\circ}$ 得到, 且点 $B$ 的对应点 $D$ 恰好落在 $B C$ 的延长线上, $A D$, 相交于点 $P$.
(1)求 $\angle B D E$ 的度数;
(2) $F$ 是 $E C$ 延长线上的点, 且 $\angle C D F=\angle D A C$.
①判断DF和PF的数量关系, 并证明;
②求证: $\frac{E P}{P F}=\frac{P C}{C F}$

因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间, 游人络绎不绝, 现有一艘游船载着游客在遗爱湖中游览. 当船在A处时, 船上游客发现岸上 $\mathrm{P} 1$ 处的临皋亭和 $P 2$ 处的遗爱亭都在东北方向; 当游船向正东方向行驶 $600 \mathrm{~m}$ 到达 $B$ 处时, 游客发现遗爱亭在北偏西 $15^{\circ}$ 方向; 当游船继续向正东方向行驶 $400 \mathrm{~m}$ 到达 $\mathrm{C}$ 处时,游客发现临皋亭在北偏西 $60^{\circ}$ 方向.
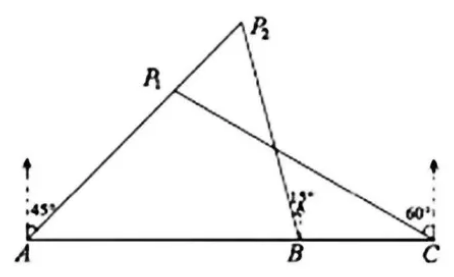
(1)求A处到临皋亭 $P$ 处的距离.
(2)求临皋亭 P1处与遗爱亭P2处之间的距离(计算结果保留根号)