单选题 (共 7 题 ),每题只有一个选项正确
设 $A, B$ 为随机事件, 则 $(A-B) \cup B$ 等于
$\text{A.}$ $A$
$\text{B.}$ $A B$
$\text{C.}$ $A \bar{B}$
$\text{D.}$ $A \cup B$
设 $A, B$ 为随机事件, $B \subset A$, 则
$\text{A.}$ $P(B-A)=P(B)-P(A)$
$\text{B.}$ $P(B \mid A)=P(B)$
$\text{C.}$ $P(A B)=P(A)$
$\text{D.}$ $P(A \cup B)=P(A)$
已知一射手在唡次独立射击中至少命中目标一次的概率为 0.96 , 则该射手每次射击的命中率为
$\text{A.}$ 0.04
$\text{B.}$ 0.2
$\text{C.}$ 0.8
$\text{D.}$ 0.96
设随机变量 $X$ 啒从犙数为 $\lambda$ 的泊松分布, 且满足 $P\{\dot{X}=1\}=\frac{2}{3} P\{X=3\}$, 则 $\lambda=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设二维随机变量 $(X, Y)$ 的分布律
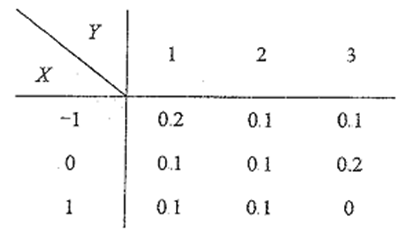
则 $P\{X+Y \leq 1\}=$
$\text{A.}$ 0.4
$\text{B.}$ 0.3
$\text{C.}$ 0.2
$\text{D.}$ 0.1
设 $x_1, x_2, \cdots, x_n$ 是来自正态总体 $N\left(\mu, \sigma^2\right)$ 的样本, $\bar{x}, s^2$ 分别为样本均值和样本方差,则 $\frac{(n-1) s^2}{\sigma^2} \sim$
$\text{A.}$ ${\chi}^2(n-1)$
$\text{B.}$ $\chi^2(n)$
$\text{C.}$ $t(n-1)$
$\text{D.}$ $t(n)$
设随机变量 $X_1, X_2, \cdots, X_{100}$ 独立同分布, $E\left(X_i\right)=0, D\left(X_1\right)=1, i=1,2, \cdots, 100$,则由中心极限定理得 $P\left\{\sum_{i=1}^{100} X_i \leq 10\right\}$ 近似于
$\text{A.}$ 0
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $\Phi(10)$
$\text{D.}$ $\Phi(100)$
填空题 (共 13 题 ),请把答案直接填写在答题纸上
从数字 $1,2, \cdots, 10$ 中有放回地任取 4 个数字, 则数字 10 恰好出现两次的概率为
设二维随机变量 $(X, Y)$ 的分布律为
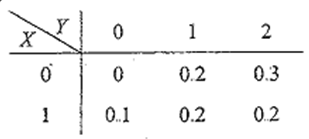
则 $P\{Y=2\}=$
设随机变最 $X$ 服从参数为 2 的泊松分布, 则 $E(2 X)=$
设随机变量 $X \sim N(1,4)$, 则 $D(X)=$
设 $x_1, x_2, \cdots, x_{10}$ 为来自总体 $X$ 的样本, 且 $X \sim N\left(1,2^2\right), \bar{x}$ 为样本均值,则 $D(\bar{x})=$
在单边假设检验中, 原假设为 $H_0: \mu \leq \mu_0$, 则其备择假设为 $H_1$ :
设总体 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right)$, 其中 $\sigma^2$ 未知, $x_1, x_2, \cdots, x_n$ 为其样本. 若假设检验问题为 $H_0: \mu=\mu_0, H_1: \mu \neq \mu_0$, 则采用的检验统计量表达现应为
设一元线性回归模型为 $y_i=\beta_0+\beta_1 x_i+\varepsilon_i, i=1,2, \cdots, n$, 则 $E\left(\varepsilon_i\right)=$.
设 $A, B$ 为随机事汼, $P(A)=0.2, P(B \mid A)=0.4, P(A \mid B)=0.5$.
求: (1) $P(A B)$;
(2) $P(A \cup B)$.
设随机变量 $X$ 的概率密度为
$$
f(x)=\left\{\begin{array}{lc}
x, & 0 \leq x < 1, \\
\frac{1}{2}, & 1 \leq x < 2, \\
0, & \text { 其他, }
\end{array}\right.
$$
求 $X$ 的分布函数 $F(x)$.
设二维随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
c x, & 0 < x < 1, \quad 0 < y < 1, \\
0, & \text { 其他, }
\end{array}\right.
$$
(1)求常数 $c$;
(2) 求 $(X, Y)$ 分别关于 $X, Y$ 的边缘摡率密度;
(3) 试问 $X$ 与 $Y$ 是否相互独立, 为什么?
设随机变量$X$的分布律为
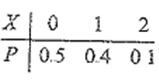
记$ Y=X^2$,
求 (1)$ D(X), D(Y)$ (2)$\operatorname{Cov}(X, Y)$
某电子元件的使用寿命 $X$ (单位: 小时) 服从参数为 $\lambda$ 的指数分布, 其概率密度为 $f(x ; \lambda)=\left\{\begin{array}{ll}\lambda \mathrm{e}^{-\lambda x}, & x>0, \\ 0, & x \leq 0,\end{array}, \lambda>0\right.$. 现抽取 $n$ 个电子元件, 测得其平均使用寿命 $\bar{x}=1000$,求 $\lambda$ 的极大似然估计.