单选题 （共 7 题 ），每题只有一个选项正确
下列各图给出了通电导体中磁感线方向或者小磁针 $\mathrm{N}$ 极指向描述正确的
$\text{A.}$ 
$\text{B.}$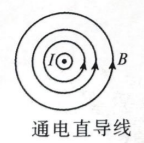 
$\text{C.}$ 
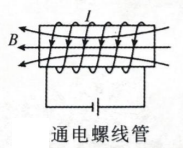$\text{D.}$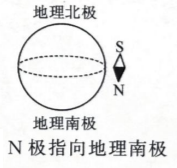 
关于电磁感应, 下列说法正确的是
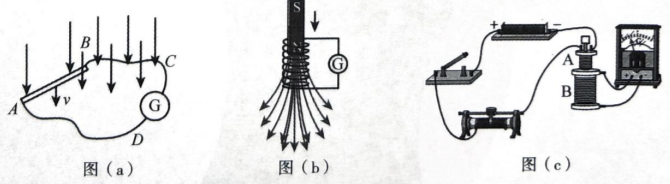
$\text{A.}$ 如图 (a) 所示, 导体 $A B$ 顺着磁感线运动, 回路中有感应电流
$\text{B.}$ 如图 (b) 所示, 条形磁铁插人线圈中不动, 有感应电流产生
$\text{C.}$ 如图 (c) 所示, 开关一直接通, 小螺线管 A 插人大螺线管 B 中不动, 滑动变阻器阻值匀速滑动时无感应电流, 加速滑动时有感应电流
$\text{D.}$ 如图 (c) 所示, 开关一直接通, 小螺线管 A 插人大螺线管 B 中不动, 只要移动滑片, 电路中就有感应电流
将质量为 $1 \mathrm{~kg}$ 的小球以 $20 \mathrm{~m} / \mathrm{s}$ 的初速度坚直向上抛出, 不计空气阻力, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 以下判断正确的是
$\text{A.}$ 小球从被抛出至到达最高点受到的冲量大小为 $10 \mathrm{~N} \cdot \mathrm{s}$
$\text{B.}$ 小球从被抛出至落回出发点动量的变化量大小为零
$\text{C.}$ 小球从被抛出至落回出发点受到的冲量大小为 $20 \mathrm{~N} \cdot \mathrm{s}$
$\text{D.}$ 小球从被抛出至落回出发点动量的变化量大小为 $40 \mathrm{~N} \cdot \mathrm{s}$
如图所示, 质量为 $m$ 的滑块沿倾角为 $\theta$ 的固定斜面向上滑动, 经过时间 $t_1$, 速度为零并又开始下滑, 经过时间 $t_2$ 回到斜面底端, 滑块在运动过程中受到的摩擦力大小始终为 $F_f$, 重力加速度为 $g$. 在整个运动过程中, 下列说法正确的是
$\text{A.}$ 支持力对滑块的总冲量为 $m g\left(t_1+t_2\right) \sin \theta$
$\text{B.}$ 重力对滑块的总冲量为 $m g\left(\mathrm{t}_1+\mathrm{t}_2\right)$
$\text{C.}$ 合外力的冲量为 0
$\text{D.}$ 摩擦力的总冲量为 $F_f\left(t_1+t_2\right)$
如图, 水平弹簧右端固定在坚直墙壁上, 左端连接在物块上, 水平面光滑. 开始时物块静止, 弹簧处于原长. 一颗子弹以水平速度 $v_0$ 射人物块, 并留在物块中. 若子弹和物块作用时间极短,下列有关说法中正确的是
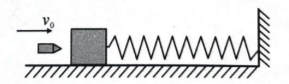
$\text{A.}$ 从子弹开始打物块到弹簧压缩至最短, 子弹、物块、弹簧组成的系统动量守恒
$\text{B.}$ 从子弹开始打物块到弹簧压缩至最短, 子弹、物块、弹簧组成的系统机械能守恒
$\text{C.}$ 从子弹开始打物块到与物块共速, 子弹、物块组成的系统动量守恒
$\text{D.}$ 子弹和物块一起压缩弹簧的过程中, 物块、子弹、弹簧组成的系统动量守恒
下列说法不正确的是
$\text{A.}$ 听到迎面而来越来越尖锐的汽笛声, 这是波的多普勒效应
$\text{B.}$ 变化的磁场能产生电场, 变化的电场也能产生磁场
$\text{C.}$ 围绕振动的音叉转一圈会听到忽强忽弱的声音, 这是声音的衍射现象
$\text{D.}$ 红外线、 $\mathrm{X}$ 射线、紫外线、可见光都是电磁波
某弹簧振子沿 $x$ 轴的简谐振动图像如图所示, 下列描述正确的是
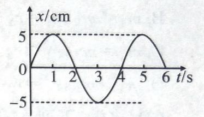
$\text{A.}$ $t=1.5 \mathrm{~s}$ 时, 振子的速度为正, 加速度为负
$\text{B.}$ $t=2.5 \mathrm{~s}$ 时, 振子的速度为负, 加速度为负
$\text{C.}$ $t=2 \mathrm{~s}$ 至 $3 \mathrm{~s}$ 时, 振子的速度越来越小, 加速度越来越大
$\text{D.}$ $t=3.5 \mathrm{~s}$ 时, 振子的速度为正, 加速度为负
多选题 （共 3 题 ），每题有多个选项正确
一列简谐横波沿 $x$ 轴传播, $t=0$ 时的波形如图所示, 质点 $A$ 与质点 $B$ 相距 $1 \mathrm{~m}, A$ 点速度沿 $y$轴正方向; $t=0.05 \mathrm{~s}$ 时, 质点 $A$ 第二次到达正向最大位移处. 由此可知
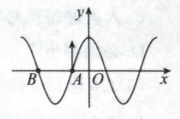
$\text{A.}$ 此波沿 $x$ 轴正方向传播
$\text{B.}$ 在 $t=0.01 \mathrm{~s}$ 时, 质点 $B$ 处在波谷位置
$\text{C.}$ 此波的传播速度为 $50 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 从 $t=0$ 时起, 经过 $0.02 \mathrm{~s}$, 质点 $A$ 沿波传播方向迁移了 $1 \mathrm{~m}$
如图所示, 斜面体静止在光滑水平面上, 将一物块轻放在斜面体顶部, 所有接触面均光滑, 关于物块下滑的过程, 下列说法正确的是
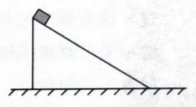
$\text{A.}$ 物块和斜面体组成的系统水平方向上动量守恒
$\text{B.}$ 物块和斜面体的动量变化量大小相等
$\text{C.}$ 斜面对物体不做功, 是因为斜面体对物体的弹力方向与斜面垂直
$\text{D.}$ 物块减少的机械能等于斜面体增加的动能
如图所示, 传送带以 $v_0=2 \mathrm{~m} / \mathrm{s}$ 的水平速度把质量 $m=20 \mathrm{~kg}$ 的行李包运送到原来静止在光滑轨道上的质量 $M=30 \mathrm{~kg}$ 的小车上 (小车足够长), 若行李包与车上表面间的动摩擦因数 $\mu=$ $0.4, \mathrm{~g}$ 取 $10 \mathrm{~m} / \mathrm{s}^2$, 则
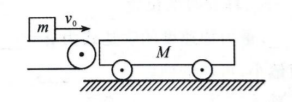
$\text{A.}$ 小车的最大速度是 $0.8 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ 车上表面越粗糙, 系统产生的内能越多
$\text{C.}$ 行李包在小车上滑动的距离为 $0.3 \mathrm{~m}$
$\text{D.}$ 行李包从滑上小车至在小车上滑到最远处的过程中小车位移为 $0.12 \mathrm{~m}$
填空题 （共 2 题 ），请把答案直接填写在答题纸上
某同学采用如图所示的装置, 利用 $\mathrm{A} 、 \mathrm{~B}$ 两球的碰撞来验证动量守恒定律. 图中 $M N$ 是斜槽, $N R$ 为水平槽. 实验时先使 $A$ 球从斜槽上某一固定位置由静止开始滚下, 落到位于水平地面的记录纸上, 留下痕迹.
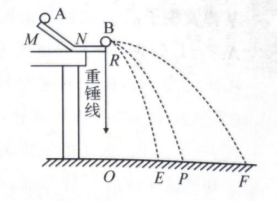
(1) $\mathrm{A}$ 球质量为 $m_1$, 半径为 $r_1$; B 球质量为 $m_2$, 半径为 $r_2$, 则
A. $m_1=m_2, r_1>r_2$
B. $m_1 < m_2, r_1=r_2$
C. $m_1=m_2, r_1 < r_2$
D. $m_1>m_2, r_1=r_2$
(2) (多选)下列不需要满足的条件是
A. 斜槽轨道末端的切线必须水平
B. 斜槽轨道必须是光滑的
C. 人射球每次必须从轨道的同一位置由静止滚下
D. 必须测出水平槽离地面的高度, 从而计算出时间
(3) (多选) 若两球间的碰撞是弹性碰撞, 下列等式正确的是
A. $m_1 O P=m_1 O E+m_2 O F$
B. $m_1 O P^2=m_1 O E^2+m_2 O F^2$
C. $m_1 O F=m_1 O E+m_2 O P$
D. $O F=O E+O P$
在 “用单摆测量重力加速度” 的实验中, 某实验小组在测量单摆的周期时, 测得摆球经过 $n$ 次全振动的总时间为 $\Delta t$, 在测量单摆的摆长时, 先用毫米刻度尺测得摆线长度为 $l$, 再用游标卡尺测量摆球的直径为 $D$.
回答下列问题:
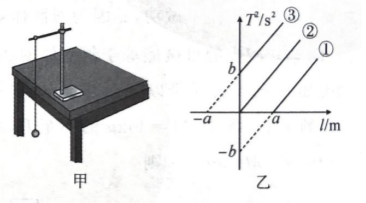
(1) 为了减小测量周期的误差, 实验时需要在适当的位置做一标记, 当摆球通过该标记时开始计时, 该标记应该放置在摆球摆动的
A. 最低点
B. 最高点
C. 任意位置
D. 开始释放时的位置
(2)该单摆的周期为 , 重力加速度的表达式为 $g=$
(3) (多选) 如果测得的 $\mathrm{g}$ 值偏小, 可能的原因是
A. 测摆长时摆线拉得过紧
B. 摆线上端悬点未固定, 振动中出现松动, 使摆线长度增加了
C. 开始计时时, 停表过迟按下
D. 实验时误将 50 次全振动记为 49 次
(4) 为了提高实验的准确度, 在实验中可改变几次摆长 $l$ 并测出相应的周期 $T$, 从而得出几组对应的 $l$ 和 $T$ 的数值, 以 $l$ 为横坐标、 $T^2$ 为纵坐标作出 $T^2-l$ 图像, 但同学们不小心每次都把摆线长当做摆长, 由此得到的 $T^2-l$ 图像是图乙中的 (选填“(1)”“(2)”或“(3)”), 由此测出的重力加速度 (选填“偏大”“偏小”或“不变”).
解答题 （共 3 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
$x$ 轴上的波源 $s_1 、 s_2$ 分别位于 $x_1=0$ 和 $x_2=1.4 \mathrm{~m}$ 处, $t=0$ 时刻两波源同时开始振动, 产生的两列简谐横波沿 $s_1 、 s_2$ 连线相向传播, $t_1=2 s$ 时两列波的图像如图所示. 质点 $M$的平衡位置位于 $x_3=0.7 \mathrm{~m}$ 处, 求:
(1) 两列波传播速度的大小;
(2) 质点 $M$ 从开始振动到 $t_2=4.5 \mathrm{~s}$ 时运动的路程.
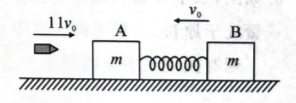
两块质量都是 $m$ 的木块 $\mathrm{A}$ 和 $\mathrm{B}$ 在光滑水平面上均以速度 $v_0$ 向左匀速运动, 中间用一根劲度系数为 $k$ 的轻弹簧连接着, 如图所示. 现从水平方向迎面射来一颗子弹, 质量为 $\frac{m}{2}$,速度为 $11 v_0$, 子弹射人木块 $\mathrm{A}$ 并留在其中. 求:
(1) 在子弹击中木块后的瞬间木块 $\mathrm{A}$ 的速度大小 $v_{\mathrm{A}}$;
(2) 若子弹击中木块时间是 $t$ ( $t$ 极小), 求子弹击中木块过程中子弹对木块 A 的平均推力 $F$;
(3) 在子弹击中木块后的运动过程中弹簧的最大弹性势能 $E_P$.
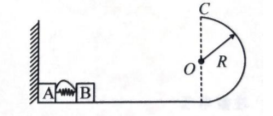
光滑水平面上放着质量 $m_{\mathrm{A}}=1 \mathrm{~kg}$ 的物块 $\mathrm{A}$ 与质量 $m_{\mathrm{B}}=2 \mathrm{~kg}$ 的物块 $\mathrm{B}, \mathrm{A}$ 与 $\mathrm{B}$ 均可视为质点, $\mathrm{A}$ 靠在坚直墙壁上, $\mathrm{A} 、 \mathrm{~B}$ 间夹一个被压缩的轻弹簧(弹簧与 $\mathrm{A} 、 \mathrm{~B}$ 均不检接), 用手挡住 $\mathrm{B}$不动, 此时弹簧弹性势能 $E_P=81 \mathrm{~J}$. 在 $\mathrm{A} 、 \mathrm{~B}$ 间系一轻质细绳, 细绳长度大于弹簧的自然长度, 如图所示. 放手后 $\mathrm{B}$ 向右运动, 绳在短暂时间内被拉断, 之后 $\mathrm{B}$ 冲上与水平面相切的坚直半圆光滑轨道, 其半径 $R=0.5 \mathrm{~m}$, B 到达最高点 $C$ 时对轨道的压力为 $44 \mathrm{~N}$. 取 $g=10 \mathrm{~m} / \mathrm{s}^2$, 求:
(1) 绳拉断后 $\mathrm{B}$ 的速度 $v_{\mathrm{B}}$ 的大小;
(2) 绳拉断过程绳对 B 的冲量 $I$ 的大小;
(3)绳拉断过程绳对 A 所做的功 $W$ 和这一过程系统损失的机械能.
