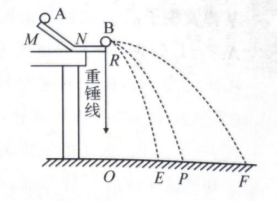
某同学采用如图所示的装置, 利用
(1)
A.
B.
C.
D.
(2) (多选)下列不需要满足的条件是
A. 斜槽轨道末端的切线必须水平
B. 斜槽轨道必须是光滑的
C. 人射球每次必须从轨道的同一位置由静止滚下
D. 必须测出水平槽离地面的高度, 从而计算出时间
(3) (多选) 若两球间的碰撞是弹性碰撞, 下列等式正确的是
A.
B.
C.
D.

(1)
A.
B.
C.
D.
(2) (多选)下列不需要满足的条件是
A. 斜槽轨道末端的切线必须水平
B. 斜槽轨道必须是光滑的
C. 人射球每次必须从轨道的同一位置由静止滚下
D. 必须测出水平槽离地面的高度, 从而计算出时间
(3) (多选) 若两球间的碰撞是弹性碰撞, 下列等式正确的是
A.
B.
C.
D.