在 “用单摆测量重力加速度” 的实验中, 某实验小组在测量单摆的周期时, 测得摆球经过 $n$ 次全振动的总时间为 $\Delta t$, 在测量单摆的摆长时, 先用毫米刻度尺测得摆线长度为 $l$, 再用游标卡尺测量摆球的直径为 $D$.
回答下列问题:

(1) 为了减小测量周期的误差, 实验时需要在适当的位置做一标记, 当摆球通过该标记时开始计时, 该标记应该放置在摆球摆动的
A. 最低点
B. 最高点
C. 任意位置
D. 开始释放时的位置
(2)该单摆的周期为 , 重力加速度的表达式为 $g=$
(3) (多选) 如果测得的 $\mathrm{g}$ 值偏小, 可能的原因是
A. 测摆长时摆线拉得过紧
B. 摆线上端悬点未固定, 振动中出现松动, 使摆线长度增加了
C. 开始计时时, 停表过迟按下
D. 实验时误将 50 次全振动记为 49 次
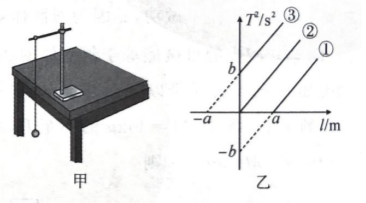
(4) 为了提高实验的准确度, 在实验中可改变几次摆长 $l$ 并测出相应的周期 $T$, 从而得出几组对应的 $l$ 和 $T$ 的数值, 以 $l$ 为横坐标、 $T^2$ 为纵坐标作出 $T^2-l$ 图像, 但同学们不小心每次都把摆线长当做摆长, 由此得到的 $T^2-l$ 图像是图乙中的 (选填“(1)”“(2)”或“(3)”), 由此测出的重力加速度 (选填“偏大”“偏小”或“不变”).