单选题 (共 11 题 ),每题只有一个选项正确
$0.010010001 \cdots\left(\right.$ 每两个 $1$ 之间依次加一个 0 ) $, 3.14, \pi, \sqrt{10},{\frac{4}{3}}$ 中有理数的个数为
$\text{A.}$ $5$ 个
$\text{B.}$ $4$ 个
$\text{C.}$ $3$ 个
$\text{D.}$ $2$ 个
在平面直角坐标系中, 点 $A(-4,-2)$ 关于 $y$ 轴对称的点的坐标是
$\text{A.}$ $(-4,2)$
$\text{B.}$ $(4,-2)$
$\text{C.}$ $(4,2)$
$\text{D.}$ $(-2,4)$
在平面直角坐标系中, 点 $A(-4,-2)$ 关于 $y$ 轴对称的点的坐标是
$\text{A.}$ $(-4,2)$
$\text{B.}$ $(4,-2)$
$\text{C.}$ $(4,2)$
$\text{D.}$ $(-2,4)$
下列各组数据中不能构成直角三角形三边长的是
$\text{A.}$ $0.7,2.4,2.5$
$\text{B.}$ $3, 4,5$
$\text{C.}$ $2, 3,4$
$\text{D.}$ $1, \sqrt{2}, \sqrt{3}$
下列二次根式中, 是最简二次根式的是
$\text{A.}$ $\sqrt{11}$
$\text{B.}$ $\sqrt{27}$
$\text{C.}$ $\sqrt{\frac{1}{2}}$
$\text{D.}$ $\sqrt{a^2}$
下列各式中正确的是
$\text{A.}$ $\sqrt{(-7)^2}=-7$
$\text{B.}$ $\sqrt{9}= \pm 3$
$\text{C.}$ $(-\sqrt{2})^2=4$
$\text{D.}$ $\sqrt{48}-\sqrt{3}=3 \sqrt{3}$
已知点 $(1, m)$ 和点 $(3, n)$ 是一次函数 $y=-2 x+3$ 图象上的两个点, 则 $m, n$ 的大小关系是
$\text{A.}$ $m>n$
$\text{B.}$ $m < n$
$\text{C.}$ $m=n$
$\text{D.}$ 以上都不对
下列正比例函数中, $y$ 的值随着 $x$ 值的增大而减小的是
$\text{A.}$ $y=0.2 x$
$\text{B.}$ $y=(\sqrt{2}-\sqrt{3}) x$
$\text{C.}$ $y=\frac{1}{5} x$
$\text{D.}$ $y=2 x$
如图, 下列条件中, 不能判断直线 $l_1 / / l_2$ 的是
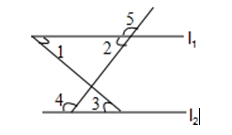
$\text{A.}$ $\angle 1=\angle 3$
$\text{B.}$ $\angle 2=\angle 3$
$\text{C.}$ $\angle 4=\angle 5$
$\text{D.}$ $\angle 2+\angle 4=180^{\circ}$
下列命题是真命题的是
$\text{A.}$ 两条直线被第三条直线所截,同旁内角互补
$\text{B.}$ 三角形内角和为$180^{\circ}$
$\text{C.}$ 三角形的一个外角等于它的两个内角之和
$\text{D.}$ 同角的余角互补
填空题 (共 8 题 ),请把答案直接填写在答题纸上
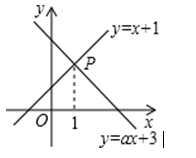
如图, 已知函数 $y=x+1$ 和 $y=a x+3$ 图象交于点 $P$, 点 $P$ 的横坐标为 $1$, 则关于 $x,y$ 的方程组 $\left\{\begin{array}{l}x-y=-1, \\ a x-y=-3\end{array}\right.$的解是
函数 ${y=k x}$ 的图象经过点 $P(-3,1)$, 则 $k$ 的值为
请你写出一个解为 $\left\{\begin{array}{l}x=2, \\ y=-4\end{array}\right.$ 的二元一次方程组
一架云梯长 2.5 米, 如图斜靠在一面墙上, 梯子的底端离墙 0.7 米, 如果梯子的顶端下滑了 0.4 米, 那么梯子的底端在水平方向滑动了 ________ 米
如图,长方形$ABCD$中,$AB=3,AD=4$,点$E$是边$BC$上一点,将$\triangle ABE$沿$AE$翻折,点$B$恰好落在对角线$AC$处,则$AE$的长为

解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\frac{1}{2} \sqrt{12}-2 \sqrt{\frac{1}{3}}+\sqrt{6} \div \sqrt{2}$
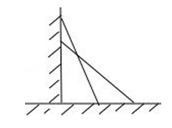
如图, 小亮将升旗的绳子拉到旗杆底端, 绳子末端刚好接触地面, 然后将绳子末端拉到距离旗杆 ${8 m}$ 处, 发现此时绳子末端距离地面 ${2 m}$, 请你求出旗杆的高度 (滑轮上方的部分忽略不计)

已知一次函数 $y=-2 x+3$, 完成下列问题:
(1)在所给直角坐标系中画出此函数的图象;
(2)图象与坐标轴交点形成的 $\triangle B O A$ 的面积是
(3)根据图象回答: 当 $x$ ________ 时, $y>1$.
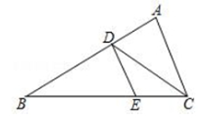
如图, 在 $\triangle A B C$ 中, $\angle A C B=70^{\circ}, \angle A=80^{\circ}, C D $ 平分 $ \angle A C B$, 且 $\angle E C D=\angle E D C$
(1)求证 $D E / / A C$;
(2) 求 ${\angle B D C}$ 的度数.
甲、乙两名队员参加射击训练(各射击 10 次), 成绩分别被制成下列两个统计图:根据以上信息, 整理分析数据如下表:

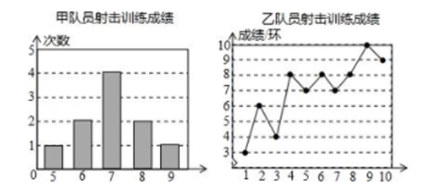
(1)写出表格中 $a, b, c$ 的值;
(2) 计算出 $d$ 的值;
(3)分别运用表中的统计量, 简要分析这两名队员的射击成绩, 若选派其中一名参赛, 你认为应选哪名队员?
某校为奖励该校在第二届学生技能大赛中表现突出的 20 名同学, 派李老师为这些同学购买奖品, 要求每人一件, 李老师到文具店看了商品后, 决定奖品在钢笔和笔记本中选择. 如果买 4 个笔记本和 2 支钢笔, 则需 86 元; 如果买 3 个笔记本和 $1$ 支钢笔, 则需 57 元.
(1) 求笔记本和钢笔的单价分别为多少元?
(2)售货员提示, 购买笔记本没有优惠: 买钢笔有优惠, 具体方法是: 如果买钢笔超过 10 支, 那么超出部分可以享受 $8$ 折优惠, 若买 $x(x>10)$ 支钢笔, 所需费用为 $y$ 元, 请你求 $y$ 与 $x$ 之间的函数关系式;
(3) 在 ${(2)}$ 的条件下, 如果买同一种奖品, 请你帮忙计算说明, 买哪种奖品费用更低.
如图,点$D$为$\triangle ABC$ 边$BC$的延长线上一点
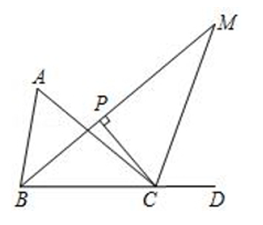
(1) 若 $3 \angle A-2 \angle A B C=20^{\circ}, \angle A C D=140^{\circ}$, 求 ${\angle A}$ 的度数;
(2) 若 $\angle A B C$ 的角平分线与 $\angle A C D$ 的角平分线交于点 $M$, 过点 $C$ 作 $C P \perp B M$ 于点 $P$, 求证: $\angle M C P=90^{\circ}-\frac{1}{2} \angle A$
(3) 在(2)条件下, $B C=5 \sqrt{2}, C M=13, B M=17$, 求 ${C P}$ 的长度.
问题背景
如图1: 在四边形 $A B C D$ 中, $A B=A D , \angle B A D=120^{\circ} , \angle B=\angle A D C=90^{\circ} . E , F$ 分别是 $B C , C D$ 上的点. 且 $\angle E A F=60^{\circ}$. 探究图中线段 $B E , E F , F D$ 之间的数量关系.
小王同学探究此问题的方法是,延长 $F D$ 到点 $G$. 使 $D G=B E$. 连接 $A G$ ,先证明 $\triangle A B E \cong \triangle A D G$ ,再证明 $\triangle A E F \cong \triangle A G F$可得出结论,他的结论应是
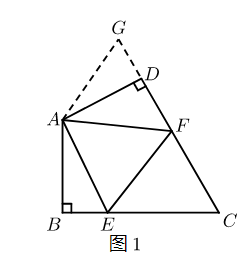
( 2 ) 探索延伸:
如图2,若在四边形 $A B C D$ 中, $A B=A D , \angle B+\angle D=180^{\circ} . E , F$ 分别是 $B C , C D$ 上的点,且 $\angle E A F=\frac{1}{2} \angle B A D$ ,上述结论是否仍然成立,并说明理由.

(3) 实际应用:
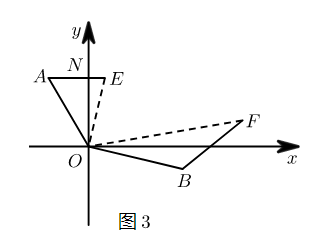
如图3,在某次军事演习中,舰艇甲在指挥中心 $\left(O\right.$ 处) 北偏西 $30^{\circ}$ 的 $A$ 处,舰艇乙在指挥中心南偏东 $70^{\circ}$ 的 $B$ 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以 60 海里/小时的速度前进,舰艇乙沿北偏东 $50^{\circ}$ 的方向以 80 海里/小时的速度进. 1.5 小时后,指挥中心观测到甲、乙两舰艇分别到达 $E , F$ 处,且两舰艇之间的夹角为 $70^{\circ}$ ,试求此时两舰艇之间的距离. (提示: 先结合图 3 ,写出已知与求证,再完成相关的说理).