问题背景
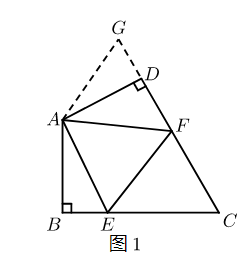
如图1: 在四边形 $A B C D$ 中, $A B=A D , \angle B A D=120^{\circ} , \angle B=\angle A D C=90^{\circ} . E , F$ 分别是 $B C , C D$ 上的点. 且 $\angle E A F=60^{\circ}$. 探究图中线段 $B E , E F , F D$ 之间的数量关系.
小王同学探究此问题的方法是,延长 $F D$ 到点 $G$. 使 $D G=B E$. 连接 $A G$ ,先证明 $\triangle A B E \cong \triangle A D G$ ,再证明 $\triangle A E F \cong \triangle A G F$可得出结论,他的结论应是
( 2 ) 探索延伸:
如图2,若在四边形 $A B C D$ 中, $A B=A D , \angle B+\angle D=180^{\circ} . E , F$ 分别是 $B C , C D$ 上的点,且 $\angle E A F=\frac{1}{2} \angle B A D$ ,上述结论是否仍然成立,并说明理由.

(3) 实际应用:
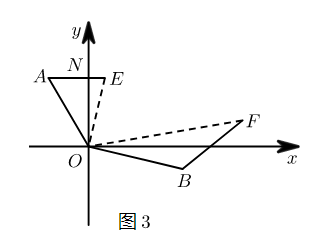
如图3,在某次军事演习中,舰艇甲在指挥中心 $\left(O\right.$ 处) 北偏西 $30^{\circ}$ 的 $A$ 处,舰艇乙在指挥中心南偏东 $70^{\circ}$ 的 $B$ 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以 60 海里/小时的速度前进,舰艇乙沿北偏东 $50^{\circ}$ 的方向以 80 海里/小时的速度进. 1.5 小时后,指挥中心观测到甲、乙两舰艇分别到达 $E , F$ 处,且两舰艇之间的夹角为 $70^{\circ}$ ,试求此时两舰艇之间的距离. (提示: 先结合图 3 ,写出已知与求证,再完成相关的说理).
如图1: 在四边形 $A B C D$ 中, $A B=A D , \angle B A D=120^{\circ} , \angle B=\angle A D C=90^{\circ} . E , F$ 分别是 $B C , C D$ 上的点. 且 $\angle E A F=60^{\circ}$. 探究图中线段 $B E , E F , F D$ 之间的数量关系.
小王同学探究此问题的方法是,延长 $F D$ 到点 $G$. 使 $D G=B E$. 连接 $A G$ ,先证明 $\triangle A B E \cong \triangle A D G$ ,再证明 $\triangle A E F \cong \triangle A G F$可得出结论,他的结论应是

( 2 ) 探索延伸:
如图2,若在四边形 $A B C D$ 中, $A B=A D , \angle B+\angle D=180^{\circ} . E , F$ 分别是 $B C , C D$ 上的点,且 $\angle E A F=\frac{1}{2} \angle B A D$ ,上述结论是否仍然成立,并说明理由.

(3) 实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心 $\left(O\right.$ 处) 北偏西 $30^{\circ}$ 的 $A$ 处,舰艇乙在指挥中心南偏东 $70^{\circ}$ 的 $B$ 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以 60 海里/小时的速度前进,舰艇乙沿北偏东 $50^{\circ}$ 的方向以 80 海里/小时的速度进. 1.5 小时后,指挥中心观测到甲、乙两舰艇分别到达 $E , F$ 处,且两舰艇之间的夹角为 $70^{\circ}$ ,试求此时两舰艇之间的距离. (提示: 先结合图 3 ,写出已知与求证,再完成相关的说理).
