单选题 （共 4 题 ），每题只有一个选项正确
若 $z=1+2 \mathrm{i}$, 则 $(1+z) \cdot \bar{z}=$
$\text{A.}$ $-2-4 i$
$\text{B.}$ $-2+4 i$
$\text{C.}$ $6-2 i$
$\text{D.}$ $6+2 {i}$
全集 $U=\mathrm{R}$, 集合 $A=\{2,3,5,7,9\}, B=\{4,5,6,8\}$, 则阴影部分表示的集合是
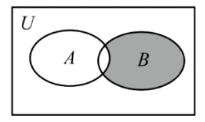
$\text{A.}$ $\{2,3,5,7,9\}$
$\text{B.}$ $\{2,3,4,5,6,7,8,9\}$
$\text{C.}$ $\{4,6,8\}$
$\text{D.}$ $\{5\}$
函数 $ f(x)=\dfrac{x \log _2|x|}{2^x+2^{-x}} $ 的部分图象大致是
$\text{A.}$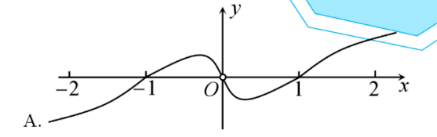 
$\text{B.}$ 
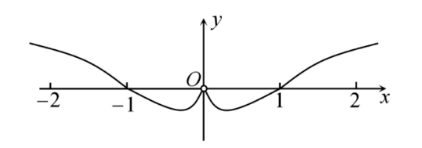$\text{C.}$ 
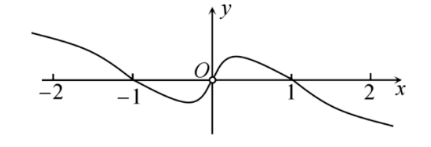$\text{D.}$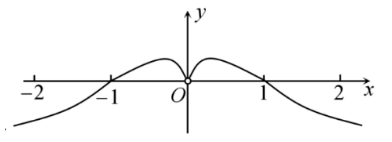 
若存在实数 $a$, 对任意的 $x \in[0, m]$, 都有 $(\sin x-a) \cdot(\cos x-a) \leqslant 0$ 恒成立, 则实数 $m$ 的最大值为
$\text{A.}$ $\frac{\pi}{4}$
$\text{B.}$ $\frac{\pi}{2}$
$\text{C.}$ $\frac{3 \pi}{4}$
$\text{D.}$ $\frac{5 \pi}{4}$
解答题 （共 3 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知正项数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且满足 $2 S_n=a_n^2+a_n$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=\frac{4}{a_n a_{n+2}}$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 证明: $T_n < 3$.
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 所对的边分别为 $a 、 b 、 c$, 已知 $\sqrt{3} b=a(\sqrt{3} \cos C-\sin C)$.
(1) 求 $A$;
(2) 若 $a=8, \triangle A B C$ 的内切圆半径为 $\sqrt{3}$, 求 $\triangle A B C$ 的周长.
混管病毒检测是应对单管病毒检测效率低下的问题, 出现的一个创新病毒检测策略,混管检测结果为阴性, 则参与该混管检测的所有人均为阴性, 混管检测结果为阳性, 则参与该混管检测的人中至少有一人为阳性. 假设一组样本有 $N$ 个人, 每个人患病毒的概率相互独立且均为 $p(0 < p < 1)$. 目前, 我们采用 $K$ 人混管病毒检测, 定义成本函数 $f(X)=\frac{N}{K}+K X$, 这里 $X$ 指该组样本 $N$ 个人中患病毒的人数.
(1) 证明: $E[f(X)] \geqslant 2 \sqrt{p} \cdot N$;
(2) 若 $0 < p < 10^{-4}, 10 \leqslant K \leqslant 20$. 证明: 某混管检测结果为阳性, 则参与该混管检测的人中大概率恰有一人为阳性.