单选题 (共 10 题 ),每题只有一个选项正确
$\left|-3^2\right|$ 的值是
$\text{A.}$ -3
$\text{B.}$ 3
$\text{C.}$ -9
$\text{D.}$ 9
-2014 的绝对值是
$\text{A.}$ $-2014$
$\text{B.}$ $2014$
$\text{C.}$ $\frac{1}{2014}$
$\text{D.}$ $-\frac{1}{2014}$
比较 $(-4)^3$ 和 $-4^3$, 下列说法正确的是
$\text{A.}$ 它们底数相同, 指数也相同
$\text{B.}$ 它们底数相同, 但指数不相同
$\text{C.}$ 它们所表示的意义相同, 但运算结果不相同
$\text{D.}$ 虽然它们底数不同, 但运算结果相同
下列关于有理数的加法说法错误的是
$\text{A.}$ 同号两数相加, 取相同的符号, 并把绝对值相加
$\text{B.}$ 异号两数相加, 绝对值相等时和为 0
$\text{C.}$ 互为相反数的两数相加得 0
$\text{D.}$ 绝对值不等时, 取绝对值较小的数的符号作为和的符号
中国航空母舰“辽宁号” 的满载排水量为 67500 吨. 将数 67500 用科学记数法表示为
$\text{A.}$ $0.675 \times 10^5$
$\text{B.}$ $6.75 \times 10^4$
$\text{C.}$ $67.5 \times 10^3$
$\text{D.}$ $675 \times 10^2$
在数轴上与 -3 的距离等于 4 的点表示的数是
$\text{A.}$ 1
$\text{B.}$ -7
$\text{C.}$ 1 或 -7
$\text{D.}$ 无数个
下列计算(1) $(-1) \times(-2) \times(-3)=6$ ;
(2) $(-36) \div(-9)=-4$; (3) $\frac{2}{3} \times\left(-\frac{9}{4}\right) \div(-1)=\frac{3}{2}$;
(4) $(-4)$ $\div \frac{1}{2} \times(-2)=16$. 其中正确的个数
$\text{A.}$ 4个
$\text{B.}$ 3个
$\text{C.}$ 2个
$\text{D.}$ 1个
设 $a$ 是最小的正整数, $b$ 是最大的负整数, $c$ 是绝对值最小的有理数, 则 $a-b-c$ 的值是
$\text{A.}$ 0
$\text{B.}$ -1
$\text{C.}$ 2
$\text{D.}$ 1
已知 $|a|=5,|b|=8$, 且 $a < b$, 则 $a+b= $
$\text{A.}$ 13 或 3
$\text{B.}$ -13 或 3
$\text{C.}$ 13 或 -3
$\text{D.}$ -13 或 -3
填空题 (共 8 题 ),请把答案直接填写在答题纸上
比较大小:
( 1$)-(-2) $ ________ $3$;
( 2 ) $-|-3.5|$ ________ $0$;
( 3 ) $-\frac{3}{4}$ ________ $-\frac{4}{5}$
计算: $(-1)^{2013}+(-1)^{2014}=$
如图, 将一刻度尺放在数轴上 (数轴的单位长度是 $1 \mathrm{~cm}$ ), 刻度尺上 “ $0 \mathrm{~cm}$ ”和 “ $8 \mathrm{~cm}$ ”分别对应数轴上的 -3 和 $x$, 那么 $x$ 的值为

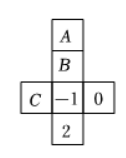
已知一个正方体的每一个表面都填有唯一一个数字, 且各相对表面上所填的数互为相反数. 若这个正方 体的表面展开图如图所示, 则 $A 、 B 、 C$ 的值分别是
若 $|m-n|=n-m$, 且 $|m|=4,|n|=3$, 则 $(m+n)^2=$
已知 $|a-2|+|b+1|+|c|=0$, 则 $a=, b=, c=$
求 $1+2+2^2+2^3+\ldots+2^{2013}$ 的值, 可令 $S=1+2+2^2+2^3+\ldots+2^{2013}$, 则 $2 S=2+2^2+2^3+\ldots+2^{2014}$, 因此 $2 S-S=2^2$ ${ }^{014}-1$. 仿照以上推理, 计算出 $1+5+5^2+5^3+\ldots+5^{2014}=$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
( 1 ) $2^2-5 \times \frac{1}{5}+|-2|$;
( 2 ) $(-2)^2-|-7|+3-2 \times\left(-\frac{1}{2}\right)$;
( 3 ) $\left(-\frac{2}{3}\right)-\left(+\frac{1}{2}\right)-\left(-\frac{5}{6}\right)-\left(-\frac{1}{3}\right)$;
( 4 ) $(-16)-(-12)-24-(-18)$.
计算:
( 1 ) $-9 \div 3+\left(\frac{1}{2}-\frac{2}{3}\right) \times 12+3^2$;
( 2 ) $(-2)^2 \times 3 \div\left(-2 \frac{2}{5}\right)-(-5)^2 \div 5 \div\left(-\frac{1}{5}\right)$.
计算: $\left(1-\frac{1}{100}\right)\left(1-\frac{1}{99}\right)\left(1-\frac{1}{98}\right) \ldots\left(1-\frac{1}{3}\right)\left(1-\frac{1}{2}\right)=$
四个数分别是 $a, b, c, d$, 满足 $|a-b|+|c-d|=\frac{1}{\mathrm{n}}|a-d|, \quad(n \geqslant 3$ 且为正整数, $a$ $ < b < c < d)$.
(1) 若 $n=3$.
①当 $d-a=6$ 时, 求 $c-b$ 的值;
②对于给定的有理数 $e(b < e < c)$, 满足 $|b-e|=\frac{4}{9}|a-d|$, 请用含 $b, c$ 的代数式 表示 $e$;
(2) 若 $e=\frac{1}{2}|b-c|, f=\frac{1}{2}|a-d|$, 且 $|e-f|>\frac{1}{10}|a-d|$, 试求 $n$ 的最大值.