单选题 (共 7 题 ),每题只有一个选项正确
安培通过实验研究, 发现了电流之间相互作用力的规律。若两段长度分别为 $\Delta l_1$ 和 $\Delta l_2$ 、 电流大小分别为 $I_1$ 和 $I_2$ 的平行直导线间距为 $r$ 时, 相互作用力的大小可以表示为 $\Delta F=k \frac{I_1 I_2 \Delta l_1 \Delta l_2}{r^2}$ 。比例系数 $k$ 的单位是
$\text{A.}$ $\mathrm{kg} \cdot \mathrm{m} /\left(\mathrm{s}^2 \cdot \mathrm{A}\right)$
$\text{B.}$ $\mathrm{kg} \cdot \mathrm{m} /\left(\mathrm{s}^2 \cdot \mathrm{A}^2\right)$
$\text{C.}$ $\mathrm{kg} \cdot \mathrm{m}^2 /\left(\mathrm{s}^3 \cdot \mathrm{A}\right)$
$\text{D.}$ $\mathrm{kg} \cdot \mathrm{m}^2 /\left(\mathrm{s}^3 \cdot \mathrm{A}^3\right)$
如图 (a), 从高处 $M$ 点到地面 $N$ 点有I、II两条光滑轨道。两相同小物块甲、乙同时 从 $M$ 点由静止释放, 沿不同轨道滑到 $N$ 点, 其速率 $v$ 与时间 $t$ 的关系如图 (b) 所示。 由图可知, 两物块在离开 $M$ 点后、到达 $N$ 点前的下滑过程中
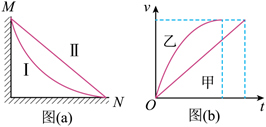
$\text{A.}$ 甲沿I下滑且同一时刻甲的动能比乙的大
$\text{B.}$ 甲沿Ⅱ下滑且同一时刻甲的动能比乙的小
$\text{C.}$ 乙沿I下滑且乙的重力功率一直不变
$\text{D.}$ 乙沿Ⅱ下滑且乙的重力功率一直增大
原子处于磁场中, 某些能级会发生辟裂。某种原子能级辟裂前后的部分能级图如图 所示, 相应能级跃迁放出的光子分别设为(1)(2)(3) (4)。若用(1)照射某金属表面时能发生光 电效应, 且逸出光电子的最大初动能为 $E_k$, 则
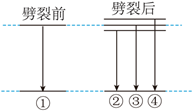
$\text{A.}$ ①和③的能量相等
$\text{B.}$ ②的频率大于④的频率
$\text{C.}$ 用②照射该金属一定能发生光电效应
$\text{D.}$ 用④照射该金属逸出光电子的最大初动能小于$E_k$
在地球上观察,月球和太阳的角直径(直径对应的张角)近似相等,如图所示。若月球绕地球运动的周期为T₁,地球绕太阳运动的周期为T₂,地球半径是月球半径的k倍,则地球与太阳的平均密度之比约为

$\text{A.}$ $k^3\left(\frac{T_1}{T_2}\right)^2$
$\text{B.}$ $k^3\left(\frac{T_2}{T_1}\right)^2$
$\text{C.}$ $\frac{1}{k^3}\left(\frac{T_1}{T_2}\right)^2$
$\text{D.}$ $\frac{1}{k^3}\left(\frac{T_2}{T_1}\right)^2$
多选题 (共 3 题 ),每题有多个选项正确
“球鼻艏”是位于远洋轮船船头水面下方的装置,当轮船以设计的标准速度航行时,球鼻艏推起的波与船首推起的波如图所示,两列波的叠加可以大幅度减小水对轮船的阻力。下列现象的物理原理与之相同的是

$\text{A.}$ 插入水中的筷子、看起来折断了
$\text{B.}$ 阳光下的肥皂膜,呈现彩色条纹
$\text{C.}$ 驶近站台的火车,汽笛音调变高
$\text{D.}$ 振动音叉的周围,声音忽高忽低
图(a)为金属四极杆带电粒子质量分析器的局部结构示意图,图(b)为四极杆内垂直于x轴的任意截面内的等势面分布图,相邻两等势面间电势差相等,则

$\text{A.}$ P点电势比M点的低
$\text{B.}$ P点电场强度大小比M点的大
$\text{C.}$ M点电场强度方向沿z轴正方向
$\text{D.}$ 沿x轴运动的带电粒子,电势能不变
如图, 两根光滑平行金属导轨固定在绝缘水平面上, 左、右两侧导轨间距分别为 $d$ 和 $2 d$, 处于坚直向上的磁场中, 磁感应强度大小分别为 $2 B$ 和 $B$ 。已知导体棒 $M N$ 的电 阻为 $R$ 、长度为 $d$, 导体棒 $P Q$ 的电阻为 $2 R$ 、长度为 $2 d, P Q$ 的质量是 $M N$ 的 2 倍。初 始时刻两棒静止, 两棒中点之间连接豕压缩量为 $L$ 的轻质绝缘弹簧。释放弹簧, 两棒在 各自磁场中运动直至停止, 弹簧始终在弹性限度内。整个过程中两榛保挂与导轨垂直并 接触良好, 导轨足够长且电阻不计。下列说法正确的足

$\text{A.}$ 弹簧伸展过程中、回路中产生顺时针方向的电流
$\text{B.}$ $P Q$ 速率为 $v$ 时, $M N$ 所受安培力大小为 $\frac{4 B^2 d^2 v}{3 R}$
$\text{C.}$ 整个运动过程中, $M N$ 与 $P Q$ 的路程之比为 $2: 1$
$\text{D.}$ 整个运动过程中, 通过 $M N$ 的电荷量为 $\frac{B L d}{3 R}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
某同学为了验证对心碰撞过程中的动量守恒定律,设计了如下实验:用纸板搭建如图所示的滑道,使硬币可以平滑地从斜面滑到水平面上,其中OA为水平段。选择相同材质的一元硬币和一角硬币进行实验。

测量硬币的质量, 得到一元和一角硬币的质量分别为 $m_1$ 和 $m_2\left(m_1>m_2\right)$ 。将硬币甲放置 在斜面一某一位置, 标记此位置为 $B$ 。由静止释放甲, 当甲停在水平面上某处时, 测量 甲从 $O$ 点到停止处的滑行距离 $O P$ 。将硬币乙放置在 $O$ 处, 左侧与 $O$ 点重合, 将甲放置 于 $B$ 点由静止释放。当两枚硬币发生碰撞后, 分别测量甲乙从 $O$ 点到停止处的滑行距 离 $O M$ 和 $O N$ 。保持释放位置不变, 重复实验若干次, 得到 $O P 、 O M 、 O N$ 的平均值分 别为 $s_0 、 s_1 、 s_2$ 。
(1) 在本实验中, 甲选用的是 ________ (填“一元”或“一角”) 硬币;
(2) 碰撞前, 甲到 $O$ 点时速度的大小可表示为 (设硬币与纸板间的动摩擦因数为 $\mu$, 重力加速度为 $g$ );
(3)若甲、乙碰撞过程中动量守恒, 则 $\frac{\sqrt{s_0}-\sqrt{s_1}}{\sqrt{s_2}}=$ (用 $m_1$ 和 $m_2$ 表示), 然后通 过测得的具体数据验证硬币对心碰撞过程中动量是否守恒;
(4) 由于存在某种系统或偶然误差, 计算得到碰撞前后思动量变化量大小与乙动量变 化量大小的比值不是 1, 写出一条产生这种误差可能的原因
导电漆是将金属粉末添加于特定树脂原料中制作而成的能导电的喷涂油漆。现有一根用导电漆制成的截面为正方形的细长样品(固态),某同学欲测量其电阻率,设计了如图(a)所示的电路图,实验步骤如下
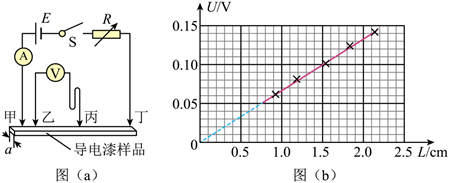
a. 测得样品截面的边长 $a=0.20 \mathrm{~cm}$;
b. 将平行排列的四根金属探针甲、乙、丙、丁与样品接触, 其中甲、乙、丁位置固定, 丙可在乙、可间左吏移动;
c. 将丙调节至某位置, 测量丙和某探针之间的距离 $L$;
d. 闭合开关 $\mathrm{S}$, 调节电阻箱 $R$ 的阻值, 使电流表示数 $I=0.40 \mathrm{~A}$, 读出相应的电压表示 数 $U$, 断开开关 $\mathrm{S}$;
e. 改变丙的位置, 重复步骤 $c 、 d$, 测量多组 $L$ 和 $U$, 作出 $U-L$ 图像如图 (b) 所示, 得到直线的斜率 $k$ 。
回答下列问题:
(1) $L$ 是丙到 (填甲乙 或丁) 的距离;
(2)写出电阻率的表达式 $\rho=$ (用 $k 、 a 、 I$ 表示);
(3) 根据图像计算出该样品的电阻率 $\rho=$ ________ $\Omega \cdot \mathrm{m}$ (保留两位有效数字)。
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某大型水陆两柄飞机具有水面滑行汲水和空中投水等功能。某次演练中, 该飞机在水而 上由静止开始|次加速直线滑行并汲水, 速度达到 $v_1=80 \mathrm{~m} / \mathrm{s}$ 时离开水面, 该过程滑行距 离 $L=1600 \mathrm{~m}$ 、汲水质量 $m=1.0 \times 10^4 \mathrm{~kg}$ 。离开水面后, 飞机琴升高度 $h=100 \mathrm{~m}$ 时速度达到 $v_2=100 \mathrm{~m} / \mathrm{s}$, 之后保持水平匀速飞行, 待接近目标时开始空中投水。取重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。求:
(1) 飞机在水面滑行阶段的加速度 $a$ 的大小及滑行时间 $t$;
(2)整个攀升阶段, 飞机汲取的水的机械能增加量 $\triangle \mathrm{E}$ 。
如图, 水平放置的两平行金属板间存在匀强电场, 板长是板间距离的 $\sqrt{3}$ 倍。金属板外 有一圆心为 $O$ 的圆形区域, 其内部存在磁感应强度大小为 $B$ 、方向垂直于纸面向外的匀 强磁场。质量为 $m$ 、电荷量为 $q(q>0)$ 的粒子沿中线以速度 $v_0$ 水平向右射入两板间, 恰好从下板边缘 $P$ 点飞出电场, 并沿 $P O$ 方向从图中 $O^{\prime}$ 点射入磁场。己知圆形磁场区域 半径为 $\frac{2 m v_0}{3 q B}$, 不计粒子重力。
(1) 求金属板间电势差 $U$;
(2) 求粒子射出磁场时与射入磁场时运动方向间的夹角 $\theta$;
(3) 仅改变圆形磁场区域的位置, 使粒子仍从图中 $O^{\prime}$ 点射入磁场, 且在磁场中的运动 时间最长。定性画出粒子在磁场中的运动轨迹及相应的弦, 标出改变后的侧形磁场区域 的圆心 $M$ 。

如图, 质量 $m_l=1 \mathrm{~kg}$ 的木板静止在光滑水平地面上, 右侧的坚直墙面固定一劲度系数 $k=$ $20 \mathrm{~N} / \mathrm{m}$ 的轻弹簧, 弹簧处于自然状态。质量 $m_2=4 \mathrm{~kg}$ 的小物块以水平向右的速度 $v_0=\frac{5}{4} \mathrm{~m} / \mathrm{s}$ 滑上木板左端, 两者共速时木板恰好与弹簧接触。木板足够长, 物块与木板 间的动摩擦因数 $\mu=0.1$, 最大静摩擦力等于滑动摩擦力。弹簧始终处在弹性限度内, 弹 簧的弹性势能 $E_p$ 与形变量 $x$ 的关系为 $E_{\mathrm{p}}=\frac{1}{2} k x^2$ 。取重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$, 结果可用 根式表示。
(1) 求木板刚接触弹簧时速度 $v$ 的大小及木板运动前右端距弹簧左端的距离 $x_I$;
(2) 求木板与弹簧接触以后, 物块与木板之间即将相对滑动时弹簧的压缩量 $x_2$ 及此时 木板速度 $v_2$ 的大小;
(3) 已知木板向右运动的速度从 $v_2$ 减小到 0 所用时间为 $t_0$ 。求木板从速度为 $v_2$ 时到之 后与物块加速度首次相同时的过程中, 系统因摩擦转化的内能 $\Delta U$ (用 $t$ 表示)。
