填空题 (共 16 题 ),请把答案直接填写在答题纸上
一质点运动的速度与路程关系为 $v=4+3 s$, 则切向加速度与路程的关系为
一个质点作半径为 $\mathrm{R}$ 的圆周运动, 角运动方程为 $\theta=4+5 t^2$, 则质点运动的切向加速度为
一个轻质弹簧, 弹性系数为 $\mathrm{k}$, 原长为 $1_0$, 现被拉长了 $\mathrm{x}$, 则 此时弹簧的弹性势能为
一理想气体的压强为 $\mathrm{p}$, 质量密度为 $\rho$, 则其平均速率为
热力学第二定律的表明一切与热现象相关的实际过程都是 (填写可逆或不可逆)。
一个电量为 $q$ 的点电荷处于一个立方体的中心处, 则通过 立方体任意一个表面的电场强度通量为
在一个半径为 $R$, 带电为 $q$ 的导体球内, 距球心 $r$ 处的场 强大小为
一个空气平行板电容器, 电容为 $\mathrm{C}$, 使用电压为 $\mathrm{v}$ 的电源 充电后与电源断开, 然后将电容器两个极板之间的距离扩大一 倍, 外力做功为
一个半径为 $R$, 载流为 $I$ 的圆弧, 所对应的圆心角为 $\pi / 2$ 。 则它在圆心产生的磁场的磁感应强度大小为
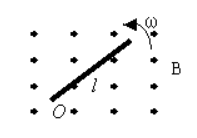
在如图所示的均匀磁场 B 中有一个载流为 $\mathrm{I}$, 半径为 $\mathrm{R}$ 的 半圆线圈。则半圆线圈所受到的磁力矩为
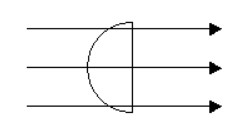
在如图所示的匀强磁场中 (磁感应强度为 B), 有一个长 为 1 的导体细棒绕过 0 点的平行于磁场的轴以角速度 $\omega$ 在垂直于 磁场的平面内转动, 则导体细棒上的动生电动势大小为
两质点沿水平轴线作相同频率和相同振幅的简谐振动。 它们每次沿相反方向经过同一个坐标为 $\mathrm{x}$ 的点时, 它们的位移 $\mathrm{x}$ 的绝对值均为振幅的一半, 则它们之间的相位差为
坚直悬挂的弹簧振子, 自然平衡时的伸长量为 $\mathrm{x}_0$, 此振 子的自由振动周期 $\mathrm{T}=$
一平面简谐机械波在媒质中传播时, 若一质元在 $\mathrm{t}$ 时刻 的波的能量是 $10 \mathrm{~J}$, 则在 ( $\mathrm{t} T$ ) ( $\mathrm{T}$ 为波的周期) 时刻该质元的振 动动能是
一束波长为 $\lambda=600 \mathrm{~nm}$ 的平行单色光垂直入射到折射率为 $n=1.33$ 的透明薄膜上, 该薄膜是放在空气中的。要使反射光得到 最大限度的加强, 薄膜最小厚度应为
用平行的白光垂直入射在平面透射光栅上时, 波长为 $\lambda_1=440 \mathrm{~nm}$ 的第 3 级光谱线, 将与波长为 ( ) 的第 2 级 光谱线重叠。
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
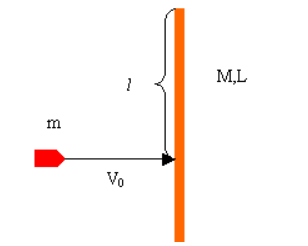
一长为 $\mathrm{L}$ 质量为 $\mathrm{M}$ 的匀质细棒, 可绕上端点处水 平轴在坚直平面内自由转动, 初始时刻静止在平衡位置。(如 图, 现有一颗质量为 $\mathrm{m}$ 的子弹以初速度 $\mathrm{v}_0$ 水平射入细棒的转轴 下方 1 处(嵌入其中)。试求细棒受到子弹打击后上摆的最大角 度。 $\left(J=m L^2 / 3\right)$
两端封闭的水平汽缸, 被一可移动活塞平分为左 右两室, 每室体积均为 $\mathrm{V}$, 其中盛有温度相同、压强均为 $\mathrm{p}$ 的同种 连续气体。现保持气体温度不变, 用外力缓慢移动活塞 (忽略摩 擦), 使左室气体的体积膨胀为右室的 2 倍, 问外力必须作多少 功?
试求一半径为 $\mathrm{R}$, 均匀带电为 $\mathrm{q}$ 的半圆周在其圆 心 0 点处的场强和电势。
有两个同心共面的圆线圈, 半径分别为 $\mathrm{R}$ 和 $\mathrm{r}$ 。 已知 $r < \left\langle\mathrm{R}\right.$, 小圆线圈中载有随时间变化的电流 $I=I_0 \sin (\omega t)$, 其 中 $I_0$ 和 $\omega$ 为已知常数。试求大圆线圈中的互感电动势。(提示: 先计算互感系数, 再计算电动势)
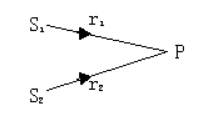
如图所示, $S_1$ 和 $S_2$ 为两相干波源。 $S_2$ 的相位比 $S_1$ 的相位超前 $\pi / 4$, 波长 $\lambda=8 \mathrm{~m}, r_1=12 \mathrm{~m}, \mathrm{r}_2=14 \mathrm{~m}, \mathrm{~S}_1$ 在 $P$ 点引起 的振动振幅为 $0.30 \mathrm{~m}, S_2$ 在 $P$ 点引起的振动振幅为 $0.20 \mathrm{~m}$, 求 $P$ 点 的合振幅
在牛顿环装置的平凸透镜和平板玻璃之间充一某种 透明液体, 观察到第 10 个明环的直径由充液前的 $14.8 \mathrm{~cm}$ 变成充 液后的 $12.7 \mathrm{~cm}$, 求这种液体的折射率 $\mathrm{n}$ 。