单选题 （共 10 题 ），每题只有一个选项正确
下列各式中, 运算正确的是
$\text{A.}$ $a^3+a^2=a^5$
$\text{B.}$ $(-a)^2 \cdot(-a)^3=a^5$
$\text{C.}$ $\left(a^2\right)^3=a^5$
$\text{D.}$ $a^3 \cdot a^2=a^5$
据悉, 世界上最小的开花结果植物是澳大利亚的出水浮萍, 这种植物的果实像一个微小 的无花果, 质量只有 $0.00000009$ 克, 将数据 $0.00000009$ 用科学记数法表示为
$\text{A.}$ $9.0 \times 10^{-8}$
$\text{B.}$ $9.0 \times 10^{-9}$
$\text{C.}$ $9.0 \times 10^8$
$\text{D.}$ $0.9 \times 10^9$
下列图形中, 由 $\angle 1=\angle 2$ 能得到 $A B / / C D$ 的是
$\text{A.}$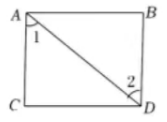 
$\text{B.}$ 
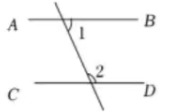$\text{C.}$ 
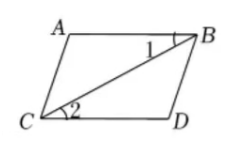$\text{D.}$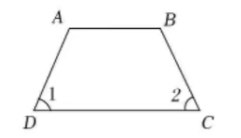 
下列多项式乘法中, 不能进行平方差计算的是
$\text{A.}$ $(x+y)(-x-y)$
$\text{B.}$ $(2 a+b)(2 a-b)$
$\text{C.}$ $(-3 x-y)(-y+3 x)$
$\text{D.}$ $\left(a^2+b\right)\left(a^2-b\right)$
数学课上, 老师提出一个问题: 经过已知角一边上的点, 做一个角等于已知角. 如图, 用尺规过 $A O B$ 的边 $O B$ 上一点 $C$ (图①) 作 $D C B A O B$ (图②). 我们可以通过以下步骤
作图:
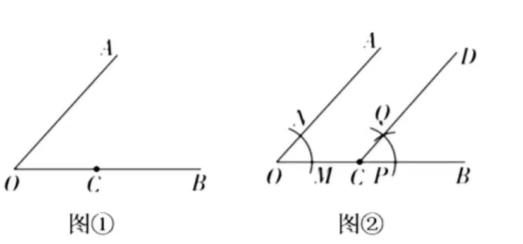
(1)作射线 $C D$;
(2)以点 $O$ 为圆心, 小于 $O C$ 的长为半径作弧, 分别交 $O A, O B$ 于点 $N, M$,
(3)以点 $P$ 为圆心, $M N$ 的长为半径作弧, 交上一段弧于点 $Q$;
(4) 以点 $C$ 为圆心, $O M$ 的长为半径作弧, 交 $O B$ 于点 $P$. 下列排序正碓的是
$\text{A.}$ (1)(2)(3)(4)
$\text{B.}$ (2)(4)(3)(1)
$\text{C.}$ (3)(2)(4) (1)
$\text{D.}$ (4)(3)(1)(2)
如图, 小亮从 $A$ 到达 $E$, 路线为 $A \rightarrow B \rightarrow C \rightarrow D \rightarrow E$. 由 $A$ 到 $B$ 和由 $D$ 到 $E$ 都是正北方向, 中间经历了 3 次拐弯, 第一次拐弯后, 行进方向变为南偏东 $40^{\circ}$, 若 $\angle D=105^{\circ}$, 则 $\angle B C D$ 的度数为
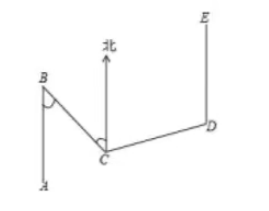
$\text{A.}$ $100^{\circ}$
$\text{B.}$ $105^{\circ}$
$\text{C.}$ $110^{\circ}$
$\text{D.}$ $115^{\circ}$
已知 $4 x^2-m x+9$ 是完全平方式, 则 $m$ 的值是
$\text{A.}$ $6$
$\text{B.}$ $9$
$\text{C.}$ $\pm 9$
$\text{D.}$ $\pm 12$
正方形的边长为 4 , 若边长增加 $x$, 那么面积增加 $y$, 则 $y$ 关于 $x$ 的函数表达式为
$\text{A.}$ $y=x^2+16$
$\text{B.}$ $y=(x+4)^2$
$\text{C.}$ $y=x^2+8 x$
$\text{D.}$ $y=16-4 x^2$
现有甲、乙两个正方形纸片, 将甲、乙并列放置后得到图 1, 已知点 $H$ 为 $A E$ 的中点, 连结 $D H, F H$. 将乙纸片放到甲的内部得到图 2. 已知甲、乙两个正方形边长之和为 6, 图 2 的阴影部分面积为 2 , 则图 1 的阴影部分面积为
$\text{A.}$ $8$
$\text{B.}$ $9$
$\text{C.}$ $10$
$\text{D.}$ $11$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
已知 $a^m=4, a^n=8$, 则 $a^{m-n}$ 的值为
已知一个角的补角是这个角的余角的 3 倍, 则这个角的度数是 度.
如图, 王老师把家里的 WIFI 密码设置成了数学问题. 吴同学来王老师家做客, 看到 $W I F I$ 图片, 思索了一会儿, 输入密码, 顺利地连接到了王老师家里的网络, 那么她输入 的密码是
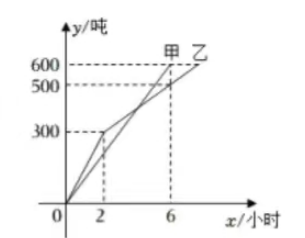
14. 甲、乙两名码头工人同时从轮船上开始卸货, 他们每人都要卸下 600 旽货物, 他们所卸 货物 $y$ (旽) 与卸货时间 $x$ (小时) 之间的关系如图所示, 则下列说法中正确的有 (填序号)
(1)甲每小时卸货 100 杶;
(2)前两个小时内, 乙每小时卸货 200 坉;
(3)乙需要 8 小时完成任务;
(4)当卸货时间为 2 小时或 6 小时时, 甲、乙两人所卸货物都相差 100 吨.
如图, 直线 $A B / / C D$, 点 $M, N$ 分别在直线 $A B, C D$ 上，点 $E$ 为直线 $A B$ 与 $C D$ 之间的 一点, 连接 $M E, N E$, 且 $\angle M E N=110^{\circ}, \angle A M E$ 的角平分线与 $\angle C N E$ 的角平分线交于 点 $F$, 则 $\angle M F N$ 的度数为
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
(1) $16 \div(-2)^3-\left(\frac{1}{3}\right)^{-1}+20$;
(2) 先化简, 再求值 $2 x(x-3)-(x+2)(x-2)$, 其中 $x=-1$.
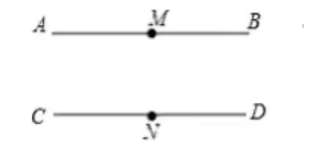
如图所示的正方形网格, 点 $A 、 B 、 C$ 都在格点上,
(1) 利用网格作图:
(1) 过点 $C$ 画直线 $A B$ 的平行线 $C D$, 并标出平行线所经过的格点 $D$;
(2)过点 $C$ 画直线 $A B$ 的垂线 $C E$, 并标出垂线所经过的格点 $E$, 垂足为点 $F$;
(2) 线段 的长度是点 $C$ 到直线 $A B$ 的距离;
(3) 比较大小: $C F$ （ ） $C B$ (填 > 、 < 或 $ = $ ), 理由是:
疫情期间, 全民检测, 人人有责. 某小区某时段进行核酸检测, 居民有序排队入场, 医 务人员开始检测后, 现场排队等待检测人数 $y$ (人) 与时间 $x$ (分钟) 之间的关系式为 $y$ $=10 x+a$, 用表格表示为:
医务人员已检测的总人数 (人) 与时间 (分钟) 之间的关系如图所示:
(1) 图中表示的自变量是
(2) 图中点 $A$ 表示的含义是
，因变量是
(3) 在医务人员开始检测 4 分钟时, 现堟阬等待检测的人数有 人;
(4) 关系式 $y=10 x+a$ 中, $a$ 的值为
(5) 医务人员开始检测 （ ） 分钟后, 现场排队等待检测人数与医务人员已检测的总
人数相同;
(6) 如果该小区共有居民 1000 人, 那么医务人员全部检测完该小区居民共需 （ ） 分 钟.
阅读下文, 寻找规律:
已知: $x \neq 1$, 观察下列各式?
$$
\begin{aligned}
& (x-1)(x+1)=x^2-1 ; \\
& (x-1)\left(x^2+x+1\right)=x^3-1 ; \\
& (x-1)\left(x^3+x^2+x+1\right)=x^4-1 ; \\
& (x-1)\left(x^4+x^3+x^2+x+1\right)=x^5-1 ; \\
& \cdots
\end{aligned}
$$
(1) 填空:
①$(x-1)\left(x^9+x^8+\cdots+x^2+x+1\right)=$
② $(1-x)\left(1+x+x^3+\cdots+x^{n-1}+x^n\right)=$
（2）根据你的猜想, 计算:
①$2^{2020}+2^{2019}+2^{2018}+\cdots+2+1=$
②那么 $2^{2020}+2^{2019}+2^{2018}+\cdots+2+1$ 的末尼数字为
【探究】
若 $x$ 满足 $(9-x)(x-4)=4$, 求 $(x-4) 2+(9-x)^2$ 的值.
设 $9-x=a, x-4=b$, 则 $(9-x)(x-4)=a b=4, a+b=(9-x)+(x-4)=5$,
$$
\therefore(9-x)^2+(x-4) 2=a^2+b^2=(a+b)^2-2 a b=5^2-2 \times 4=17 ;
$$
【应用】
请仿照上面的方法求解下面问题:
(1) 若 $x$ 满足 $(5-x)(x-2)=2$, 求 $(5-x)^2+(x-2)^2$ 的值;
【拓展】
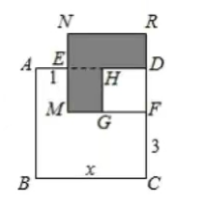
(2) 已知正方形 $A B C D$ 的边长为 $x, E, F$ 分别是 $A D 、 D C$ 上的点, 且 $A E=1, C F=3$, 长方形 $E M F D$ 的面积是 8 , 分别以 $M F 、 D F$ 为边作正方形.
(1) $M F=$，$DF=$（用含 $x$ 的式子表示）
(2)求阴影部分的面积.
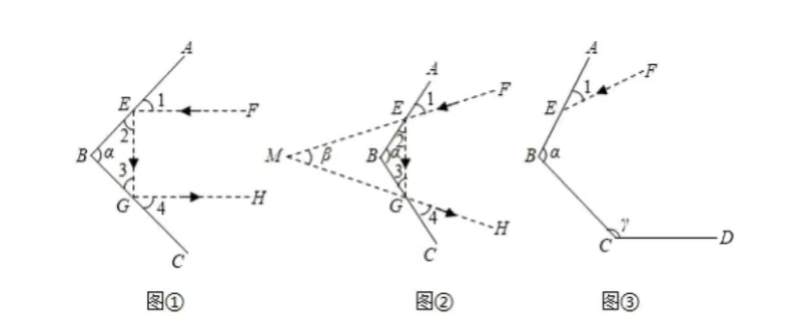
在小学我们学过三角形的内角和等于 $180^{\circ}$; 科学实验又证明, 平面镜反射光线的规律 是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等. 例如：在图(1)、图(2) 中, 都有 $\angle 1=\angle 2, \angle 3=\angle 4$. 设镜子 $A B$ 与 $B C$ 的夹角 $\angle A B C=\alpha$.
(1) 如图①, 若 $\alpha=90^{\circ}, \angle 1=50^{\circ}$, 则 $\angle 4=$
(2) 如图②, 若 $\alpha=115^{\circ}$, 入射光线 $E F$ 与反射光线 $G H$ 的夹角 $\angle F M H=\beta$. 求 $\beta$ 的度数;
(3) 如图③, 若 $90^{\circ} < \alpha < 180^{\circ}$, 设镜子 $C D$ 与 $B C$ 的夹角 $\angle B C D=\gamma\left(90^{\circ} < \gamma < 180\right.$
)), 入射光线 $E F$ 与镜面 $A B$ 的夹角 $\angle 1=m\left(0^{\circ} < m < 90^{\circ}\right)$, 已知入射光线 $E F$ 从镜面 $A B$ 反射到镜面 $B C$, 再反射到镜面 $C D$, 最后经镜面 $C D$ 反射后, 当反射光线与入射光线 $E F$ 平行时, 探索 $m$ 与 $\gamma$ 的数量关系, 并说明理由.
