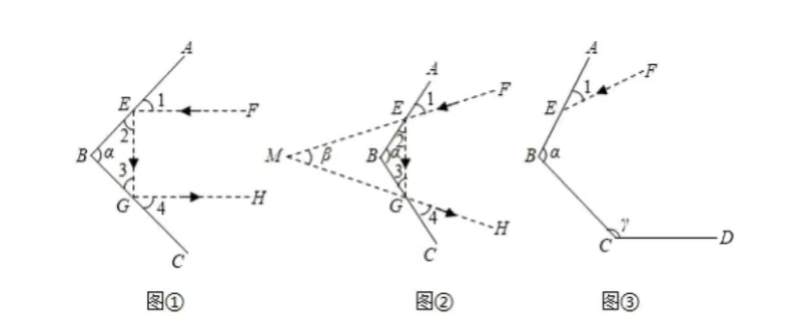
在小学我们学过三角形的内角和等于 $180^{\circ}$; 科学实验又证明, 平面镜反射光线的规律 是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等. 例如:在图(1)、图(2) 中, 都有 $\angle 1=\angle 2, \angle 3=\angle 4$. 设镜子 $A B$ 与 $B C$ 的夹角 $\angle A B C=\alpha$.
(1) 如图①, 若 $\alpha=90^{\circ}, \angle 1=50^{\circ}$, 则 $\angle 4=$
(2) 如图②, 若 $\alpha=115^{\circ}$, 入射光线 $E F$ 与反射光线 $G H$ 的夹角 $\angle F M H=\beta$. 求 $\beta$ 的度数;
(3) 如图③, 若 $90^{\circ} < \alpha < 180^{\circ}$, 设镜子 $C D$ 与 $B C$ 的夹角 $\angle B C D=\gamma\left(90^{\circ} < \gamma < 180\right.$
)), 入射光线 $E F$ 与镜面 $A B$ 的夹角 $\angle 1=m\left(0^{\circ} < m < 90^{\circ}\right)$, 已知入射光线 $E F$ 从镜面 $A B$ 反射到镜面 $B C$, 再反射到镜面 $C D$, 最后经镜面 $C D$ 反射后, 当反射光线与入射光线 $E F$ 平行时, 探索 $m$ 与 $\gamma$ 的数量关系, 并说明理由.
(1) 如图①, 若 $\alpha=90^{\circ}, \angle 1=50^{\circ}$, 则 $\angle 4=$
(2) 如图②, 若 $\alpha=115^{\circ}$, 入射光线 $E F$ 与反射光线 $G H$ 的夹角 $\angle F M H=\beta$. 求 $\beta$ 的度数;
(3) 如图③, 若 $90^{\circ} < \alpha < 180^{\circ}$, 设镜子 $C D$ 与 $B C$ 的夹角 $\angle B C D=\gamma\left(90^{\circ} < \gamma < 180\right.$
)), 入射光线 $E F$ 与镜面 $A B$ 的夹角 $\angle 1=m\left(0^{\circ} < m < 90^{\circ}\right)$, 已知入射光线 $E F$ 从镜面 $A B$ 反射到镜面 $B C$, 再反射到镜面 $C D$, 最后经镜面 $C D$ 反射后, 当反射光线与入射光线 $E F$ 平行时, 探索 $m$ 与 $\gamma$ 的数量关系, 并说明理由.
