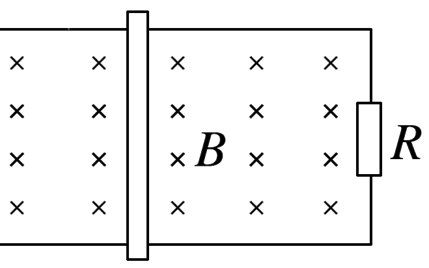单选题 (共 7 题 ),每题只有一个选项正确
在匀强磁场中,匝数 $N=100$ 的矩形线圈绕垂直磁感线的转轴匀速转动,线圈中产生的感应电动势随时间变化规律如图所示,则下列说法正确的是
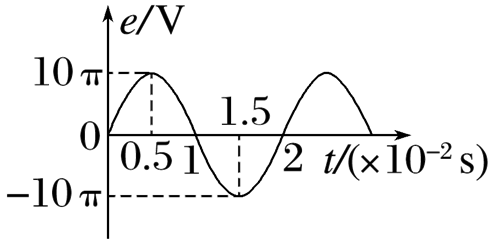
$\text{A.}$ $t=0.5 \times 10^{-2} s$ 时,线圈平面与中性面重合
$\text{B.}$ $t=1 \times 10^{-2} s$ 时,线圈中磁通量变化率最大
$\text{C.}$ 穿过每一匝线圈的最大磁通量为 $1 \times 10^{-3} Wb$
$\text{D.}$ 线圈转动的角速度为 $50 \pi rad / s$
如图是简化的某种旋转磁极式发电机原理图.定子是仅匝数n不同的两线圈,n1 > n2,二者轴线在同一平面内且相互垂直,两线圈到其轴线交点O的距离相等,且均连接阻值为R的电阻,转子是中心在O点的条形磁铁,绕O点在该平面内匀速转动时,两线圈输出正弦式交变电流.不计线圈电阻、自感及两线圈间的相互影响,下列说法正确的是
$\text{A.}$ 两线圈产生的电动势的有效值相等
$\text{B.}$ 两线圈产生的交变电流频率相等
$\text{C.}$ 两线圈产生的电动势同时达到最大值
$\text{D.}$ 两电阻消耗的电功率相等
一只低压电源输出的交变电压为 $U=10 \sqrt{2} \sin 314 t(V)$ ,$\pi$ 取3.14,以下说法正确的是
$\text{A.}$ 这只电源可以使" $10 V \quad 2 W$"的灯泡正常发光
$\text{B.}$ 这只电源的交变电压的周期是 314 s
$\text{C.}$ 这只电源在 $t=0.01 s$ 时电压达到最大值
$\text{D.}$ " $10 V 2 \mu F$"的电容器可以接在这只电源上
某研究小组成员设计了一个如图所示的电路,已知纯电阻 $R$ 的阻值不随温度变化.与 $R$ 并联的是一个理想的交流电压表,$D$ 是理想二极管(它的导电特点是正向电阻为零,反向电阻为无穷大)。在 $A 、 B$ 间加一交流电压,其瞬时值的表达式为 $u=20 \sqrt{2} \sin 100 \pi t(V)$ ,则交流电压表的示数为

$\text{A.}$ 10 V
$\text{B.}$ 20 V
$\text{C.}$ 15 V
$\text{D.}$ 14.1 V
一电阻接到方波交流电源上,在一个周期内产生的热量为 $Q_{\text {方 }}$ ;若该电阻接到正弦交流电源上,在一个周期内产生的热量为 $Q_{\text {正 } \text { 该电阻上电压的峰值均为 } u_0 \text { ,周期均为 } T \text { ,如图所示.则 } Q_{\text {方 }}: ~ Q_{\text {正等于 }} ~}^{\text {等于 }}$
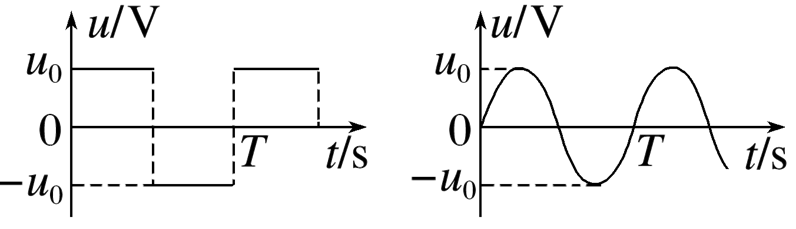
$\text{A.}$ $1: \sqrt{2}$
$\text{B.}$ $\sqrt{2}: 1$
$\text{C.}$ $1: 2$
$\text{D.}$ 2:1
如图所示,坐标系 $x O y$ 的第一、四象限的两块区域内分别存在垂直纸面向里、向外的匀强磁场,磁感应强度的大小均为 1.0 T ,两块区域曲线边界的曲线方程为 $y=0.5 \sin 2 \pi x(m)(0 \leqslant x \leqslant 1.0 m)$ 。现有一单匝矩形导线框 $a b c d$ 在拉力 $F$ 的作用下,从图示位置开始沿 $x$ 轴正方向以 $2 m / s$ 的速度做匀速直线运动,已知导线框长为 1 m 、宽为 0.5 m 、总电阻为 $1 \Omega$ ,开始时 $b c$ 边与 $y$ 轴重合。则导线框穿过两块区域的整个过程拉力 $F$ 做的功为
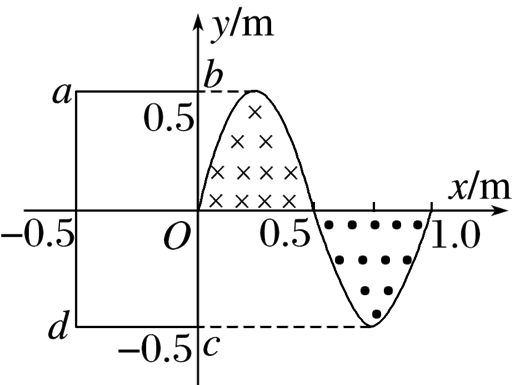
$\text{A.}$ 0.25 J
$\text{B.}$ 0.375 J
$\text{C.}$ 0.5 J
$\text{D.}$ 0.75 J
如图所示的正方形线框 $a b c d$ 的边长为 $L$ ,每边电阻均为 $r$ ,在垂直于纸面向里、磁感应强度大小为 $B$ 的匀强磁场中绕 $c d$ 轴以角速度 $\omega$ 匀速转动,$c 、 d$ 两点与一阻值为 $r$ 的电阻相连,各表均可视为理想电表,导线电阻不计,则下列说法中正确的是
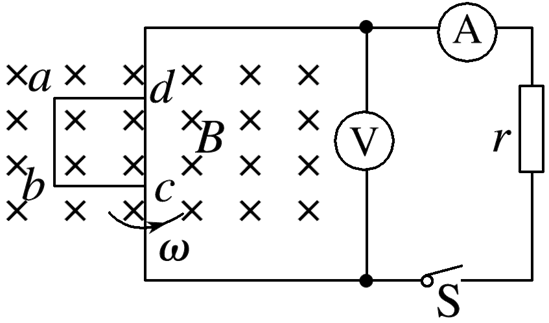
$\text{A.}$ 线框 $a b c d$ 产生的电流为交变电流
$\text{B.}$ 当 $S$ 断开时,电压表的示数为零
$\text{C.}$ 当 S 断开时,电压表的示数为 $\frac{\sqrt{2}}{8} B \omega L^2$
$\text{D.}$ 当 S 闭合时,电流表的示数为 $\frac{\sqrt{2} B \omega L^2}{14 r}$
多选题 (共 4 题 ),每题有多个选项正确
如图所示,图线 $a$ 是线圈在匀强磁场中匀速转动时所产生正弦式交变电流的图像,当调整线圈转速后,其在同一磁场中匀速转动过程所产生正弦式交变电流的图像如图线 $b$ 所示.下列关于这两个正弦式交变电流的说法中正确的是
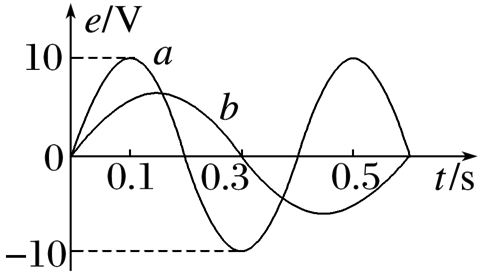
$\text{A.}$ 在图中 $t=0$ 时刻穿过线圈的磁通量均为零
$\text{B.}$ 线圈先后两次转速之比为 $3: 2$
$\text{C.}$ 交变电流 $a$ 的电动势瞬时值表达式为 $e=10 \sin (5 \pi t) V$
$\text{D.}$ 交变电流 $b$ 的电动势最大值为 $\frac{20}{3} V$
如图所示,一个半径为r的半圆形线圈,以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直)的匀强磁场,磁感应强度大小为B.M和N是两个集流环,负载电阻为R,线圈、电流表和连接导线的电阻不计,若图示位置为初始时刻,则

$\text{A.}$ 感应电动势的最大值为 $2 \pi^2 B n r^2$
$\text{B.}$ 从图示位置起到转过 $\frac{1}{4}$ 转的时间内,负载电阻 $R$ 上产生的热量为 $\frac{\pi^4 B^2 n r^4}{8 R}$
$\text{C.}$ 从图示位置起到转过 $\frac{1}{4}$ 转的时间内,通过负载电阻 $R$的电荷量为 $\frac{\pi B r^2}{2 R}$
$\text{D.}$ 电流表的示数为 $\frac{\pi^2 r^2 n B}{2 R}$
如图所示,发电机内部线圈处于磁体和圆柱形铁芯之间的径向磁场中,磁体的 $N 、 S$ 极间的过渡区域宽度很小,可忽略不计。线圈的匝数为 $N$ 、面积为 $S$ 、总电阻为 $r$ ,线圈所在位置的磁感应强度大小为 $B$ 。当线圈以角速度 $\omega$ 匀速转动时,额定电压为 $U$ 、电阻为 $R$ 的小灯泡在电路中恰能正常发光,则

$\text{A.}$ 发电机输出的电流为矩形波交流电
$\text{B.}$ 灯泡两端电压 $U=\frac{\sqrt{2}}{2} N B S \omega$
$\text{C.}$ 感应电动势的有效值是 $\left(1+\frac{r}{R}\right) U$
$\text{D.}$ 转动过程中穿过线圈的磁通量始终为零
如图甲所示,电阻不计、面积 $S=0.04 m^2$ 的固定矩形线圈水平放置,与线圈平面垂直的空间有均匀分布的匀强磁场,磁场的磁感应强度随时间变化的规律如图乙所示.此时与线圈连接的额定电压是 40 V 的灯泡正常发光,氖泡两端瞬时电压达到 40 V 时开始发光.下列说法正确的是(不计灯丝电阻随温度的变化)
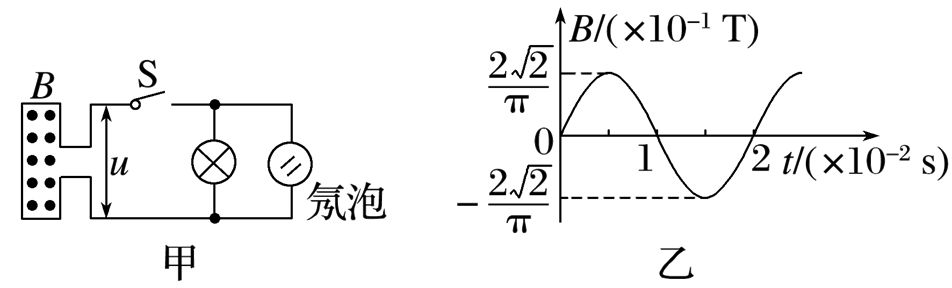
$\text{A.}$ 氖泡两端电压的瞬时值表达式为$u=40 \sqrt{2} \cdot \cos 100 \pi t(V)$
$\text{B.}$ 矩形线圈匝数 $N=50$ 匝
$\text{C.}$ 氖泡的发光频率为 50 Hz
$\text{D.}$ 若将氖泡换成一个耐压值为 40 V 的电容器,电容器可以安全工作
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示,间距为 $L$ 的光滑平行金属导轨,水平地放置在坚直向上且磁感应强度大小为 $B$ 的匀强磁场中,一端接阻值为 $R$ 的电阻。一有效电阻为 $r$ 、质量为 $m$ 的导体棒放置在导轨上,在外力 $F$ 作用下从 $t=0$ 时刻开始运动,其速度随时间的变化规律为 $v=v_{ m } \sin \omega t$ ,不计导轨电阻。求:
(1)从 $t=0$ 到 $t=\frac{2 \pi}{\omega}$ 时间内,电阻 $R$ 上产生的热量;
(2)从 $t=0$ 到 $t=\frac{2 \pi}{\omega}$ 时间内,外力 $F$ 所做的功.