单选题 (共 5 题 ),每题只有一个选项正确
如图所示是两个相互连接的金属圆环,小金属环的电阻是大金属环电阻的二分之一,匀强磁场垂直穿过大金属环所在区域,当磁感应强度随时间均匀变化时,在大环内产生的感应电动势为 $E$ ,则 $a 、 b$ 两点间的电势差为
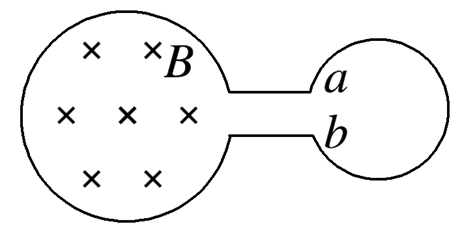
$\text{A.}$ $\frac{1}{2} E$
$\text{B.}$ $\frac{1}{3} E$
$\text{C.}$ $\frac{2}{3} E$
$\text{D.}$ $E$
如图所示,线圈匝数为n,横截面积为S,线圈电阻为R,处于一个均匀增强的磁场中,磁感应强度随时间的变化率为k,磁场方向水平向右且与线圈平面垂直,电容器的电容为C,两个电阻的阻值均为2R.下列说法正确的是

$\text{A.}$ 电容器上极板带负电
$\text{B.}$ 通过线圈的电流大小为 $\frac{n k S}{2 R}$
$\text{C.}$ 电容器所带的电荷量为 $\frac{C n k S}{2}$
$\text{D.}$ 电容器所带的电荷量为 $\frac{2 C n k S}{3}$
如图甲所示,一长为 $L$ 的导体棒,绕水平圆轨道的圆心 $O$匀速顺时针转动,角速度为 $\omega$ ,电阻为 $r$ ,在圆轨道空间存在有界匀强磁场,磁感应强度大小为 $B$ 。半径小于 $\frac{L}{2}$ 的区域内磁场坚直向上,半径大于 $\frac{L}{2}$ 的区域内磁场坚直向下,俯视图如图乙所示,导线一端 $Q$ 与圆心 $O$ 相连,另一端 $P$ 与圆轨道连接给电阻 $R$ 供电,其余电阻不计,则
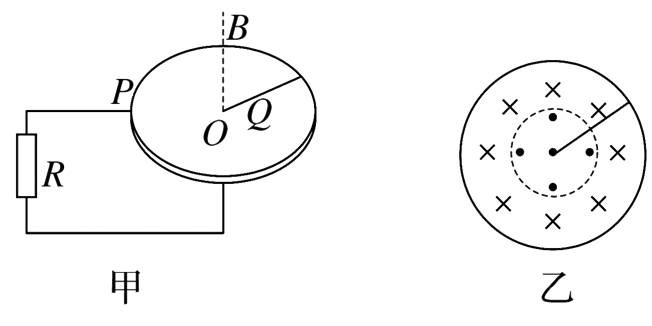
$\text{A.}$ 电阻 $R$ 两端的电压为 $\frac{B L^2 \omega}{4}$
$\text{B.}$ 电阻 $R$ 中的电流方向向上
$\text{C.}$ 电阻 $R$ 中的电流大小为 $\frac{B L^2 \omega}{4(R+r)}$
$\text{D.}$ 导体棒的安培力做功的功率为 0
多选题 (共 4 题 ),每题有多个选项正确
如图所示,在磁感应强度大小为 $B$ 、方向坚直向下的匀强磁场中,有两根光滑的平行导轨,间距为 $L$ ,导轨两端分别接有电阻 $R_1$ 和 $R_2$ ,导体棒以某一初速度从 $a b$ 位置向右运动距离 $x$ 到达 $c d$ 位置时,速度为 $v$ ,产生的电动势为 $E$ ,此过程中通过电阻 $R_1 、 R_2$ 的电荷量分别为 $q_1 、 q_2$ .导体棒有电阻,导轨电阻不计.下列关系式喀正确的是
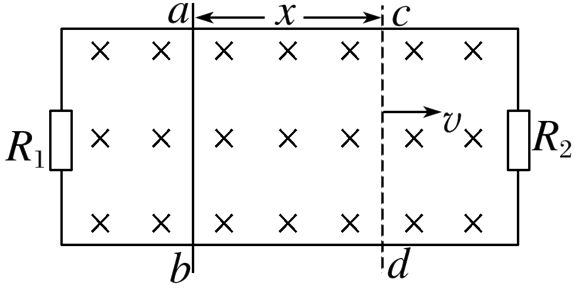
$\text{A.}$ $E_0=B L v$
$\text{B.}$ $E=2 B L v$
$\text{C.}$ $q_1=\frac{B L x}{R_1}$
$\text{D.}$ $\frac{q_1}{q_2}=\frac{R_2}{R_1}$
如图甲所示,单匝正方形线框 $a b c d$ 的电阻 $R=0.5 \Omega$ ,边长 $L=20 cm$ ,匀强磁场垂直于线框平面向里,磁感应强度的大小随时间变化规律如图乙所示,则下列说法中正确的是
为 $4.8 \times 10^{-2} C$
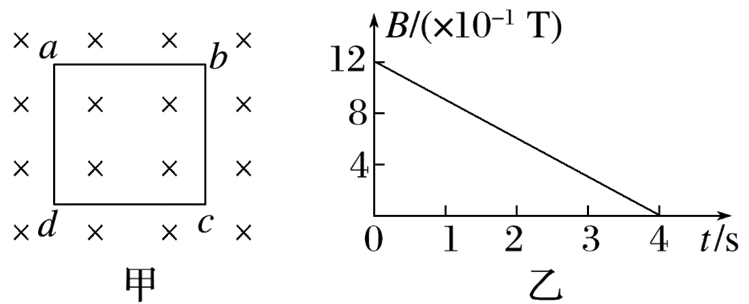
$\text{A.}$ 线框中的感应电流沿逆时针方向,大小为 $2.4 \times 10^{-2} A$
$\text{B.}$ $0 \sim 2 s$ 内通过 $a b$ 边横截面的电荷量
$\text{C.}$ 3 s时 $a b$ 边所受安培力的大小为 $1.44 \times 10^{-2} N$
$\text{D.}$ $0 \sim 4 s$ 内线框中产生的焦耳热为 $1.152 \times 10^{-3} J$
如图,$P A Q$ 为一段固定于水平面上的光滑圆弧导轨,圆弧的圆心为 $O$ ,半径为 $L$ .空间存在垂直导轨平面、磁感应强度大小为 $B$ 的匀强磁场。电阻为 $R$ 的金属杆 $O A$ 与导轨接触良好,图中电阻 $R_1=R_2=R$ ,其余电阻不计。现使 $O A$ 杆在外力作用下以恒定角速度 $\omega$ 绕圆心 $O$ 顺时针转动,在其转过 $\frac{\pi}{3}$ 的过程中,下列说法正确的是
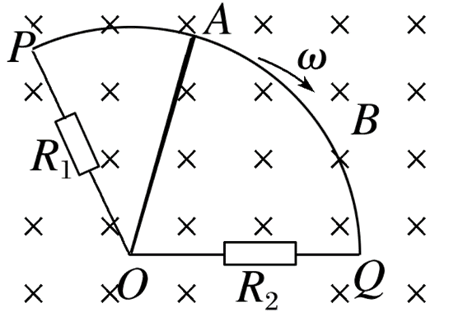
$\text{A.}$ 流过电阻 $R_1$ 的电流方向为 $P \rightarrow R_1 \rightarrow O$
$\text{B.}$ $A 、 O$ 两点间电势差为 $\frac{B L^2 \omega}{2}$
$\text{C.}$ 流过 $O A$ 的电荷量为 $\frac{\pi B L^2}{6 R}$
$\text{D.}$ 外力做的功为 $\frac{\pi \omega B^2 L^4}{18 R}$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图甲所示,虚线MN左、右两侧的空间均存在与纸面垂直的匀强磁场,右侧匀强磁场的方向垂直纸面向外,磁感应强度大小恒为B0;左侧匀强磁场的磁感应强度B随时间t变化的规律如图乙所示,规定垂直纸面向外为磁场的正方向.一硬质细导线的电阻率为ρ、横截面积为S0,将该导线做成半径为r的圆环固定在纸面内,圆心O在MN上.求:
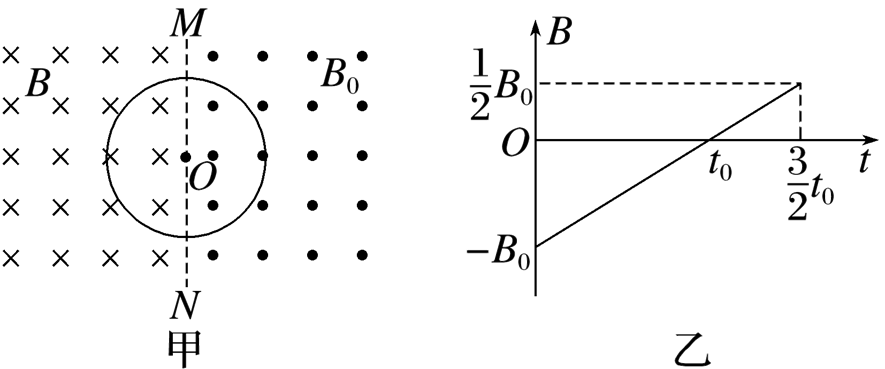
(1)$t=\frac{t_0}{2}$ 时,圆环受到的安培力;
(2)在 $0 \sim \frac{3}{2} t_0$ 内,通过圆环的电荷量.
如图所示,光滑的足够长的平行水平金属导轨 $M N 、 P Q$ 相距 $l$ ,在 $M 、 P$ 和 $N 、$ $Q$ 间各连接一个额定电压为 $U$ 、阻值恒为 $R$ 的灯泡 $L _1 、 L_2$ ,在两导轨间 $c d f e$ 矩形区域内有垂直导轨平面坚直向上、宽为 $d_0$ 的有界匀强磁场,磁感应强度为 $B_0$ ,且磁场区域可以移动,一电阻也为 $R$ 、长度大小也刚好为 $l$ 的导体棒 $a b$ 垂直固定在磁场左边的导轨上,离灯泡 $L _1$ 足够远.现让匀强磁场在导轨间以某一恒定速度向左移动,当棒 $a b$ 刚处于磁场时两灯泡恰好正常工作.棒 $a b$ 与导轨始终保持良好接触,导轨电阻不计.
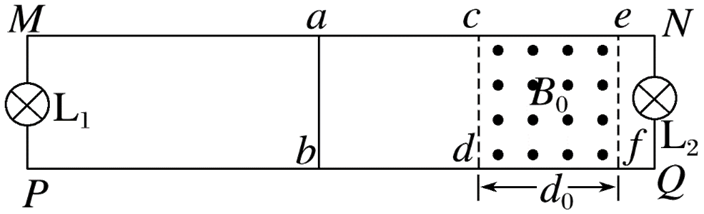
(1)求磁场移动的速度大小;
(2)若保持磁场不移动(仍在 $c d f e$ 矩形区域),而使磁感应强度 $B$ 随时间 $t$ 均匀变化,两灯泡中有一灯泡正常工作且都有电流通过,设 $t=0$ 时,磁感应强度为 $B_0$ .试求出经过时间 $t$ 时磁感应强度的可能值 $B_t$ .