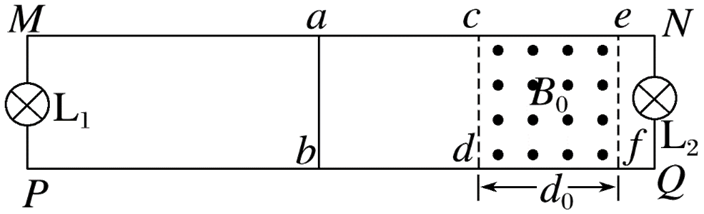
如图所示，光滑的足够长的平行水平金属导轨 $M N 、 P Q$ 相距 $l$ ，在 $M 、 P$ 和 $N 、$ $Q$ 间各连接一个额定电压为 $U$ 、阻值恒为 $R$ 的灯泡 $L _1 、 L_2$ ，在两导轨间 $c d f e$ 矩形区域内有垂直导轨平面坚直向上、宽为 $d_0$ 的有界匀强磁场，磁感应强度为 $B_0$ ，且磁场区域可以移动，一电阻也为 $R$ 、长度大小也刚好为 $l$ 的导体棒 $a b$ 垂直固定在磁场左边的导轨上，离灯泡 $L _1$ 足够远．现让匀强磁场在导轨间以某一恒定速度向左移动，当棒 $a b$ 刚处于磁场时两灯泡恰好正常工作．棒 $a b$ 与导轨始终保持良好接触，导轨电阻不计．



(1)求磁场移动的速度大小；

（2）若保持磁场不移动（仍在 $c d f e$ 矩形区域），而使磁感应强度 $B$ 随时间 $t$ 均匀变化，两灯泡中有一灯泡正常工作且都有电流通过，设 $t=0$ 时，磁感应强度为 $B_0$ ．试求出经过时间 $t$ 时磁感应强度的可能值 $B_t$ ．