单选题 (共 6 题 ),每题只有一个选项正确
张衡是中国东汉时期伟大的天文学家、数学家,他曾经得出圆周率的平方除以十六等于八分之五.已知三棱锥 $A-B C D$ 的每个顶点都在球 $O$ 的球面上,$A B \perp$ 底面 $B C D, B C \perp C D$ ,且 $A B=C D=\sqrt{3}, B C=2$ ,利用张衡的结论可得球 $O$ 的表面积为( )
$\text{A.}$ 30
$\text{B.}$ $10 \sqrt{10}$
$\text{C.}$ 33
$\text{D.}$ $12 \sqrt{10}$
已知边长为 2 的等边三角形 $A B C, D$ 为 $B C$ 的中点,以 $A D$ 为折痕进行折叠,使折后的 $\angle B D C=\frac{\pi}{2}$ ,则过 $A, B, C, D$ 四点的球的表面积为( )
$\text{A.}$ $3 \pi$
$\text{B.}$ $4 \pi$
$\text{C.}$ $5 \pi$
$\text{D.}$ $6 \pi$
已知三棱锥 $P-A B C$ 的四个顶点都在球 $O$ 的球面上,$P B=P C=2 \sqrt{5}, A B=A C=4$ , $P A=B C=2$ ,则球 $O$ 的表面积为
$\text{A.}$ $\frac{316}{15} \pi$
$\text{B.}$ $\frac{79}{15} \pi$
$\text{C.}$ $\frac{158}{5} \pi$
$\text{D.}$ $\frac{79}{5} \pi$
我国古代建筑的屋顶对建筑立面起着特别重要的作用,古代建筑屋顶主要有庑殿式、硬山顶、歇山顶、悬山顶攒尖顶、盝顶、卷棚顶等类型,其中硬山式屋顶造型的最大特点是比较简单、朴素,只有前后两面坡,而且屋顶在山墙墙头处与山墙齐平,没有伸出部分,山面裸露没有变化.硬山式屋顶(如图 1)可近似地看作直三棱柱(如图 2),其高为 $10 m, C C_1$ 到平面 $A B B_1 A_1$的距离为 $1.5 m, A B$ 为 4 m ,则可估算硬山式屋顶的体积约为
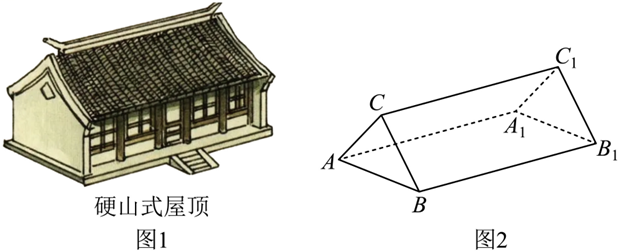
$\text{A.}$ $15 m^3$
$\text{B.}$ $30 m^3$
$\text{C.}$ $45 m^3$
$\text{D.}$ $60 m^3$
已知一圆台高为 7 ,下底面半径长 4 ,此圆台外接球的表面积为 $100 \pi$ ,则此圆台的体积为
$\text{A.}$ $84 \pi$
$\text{B.}$ $86 \pi$
$\text{C.}$ $\frac{259}{3} \pi$
$\text{D.}$ $\frac{262}{3} \pi$
已知菱形 $A B C D$ 的各边长为 $2, \angle B=60^{\circ}$ .将 $ A B C$ 沿 $A C$ 折起,折起后记点 $B$ 为 $P$ ,连接 $P D$ ,得到三棱锥 $P-A C D$ ,如图所示,当三棱锥 $P-A C D$ 的表面积最大时,三棱锥 $P-A C D$ 的外接球体积为
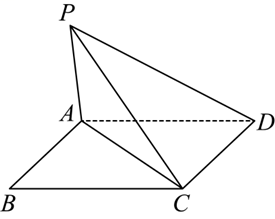
$\text{A.}$ $\frac{5 \sqrt{2}}{3} \pi$
$\text{B.}$ $\frac{4 \sqrt{3}}{3} \pi$
$\text{C.}$ $2 \sqrt{3} \pi$
$\text{D.}$ $\frac{8 \sqrt{2}}{3} \pi$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
如图,在圆柱 $O_1 O_2$ 内有一个球 $O$ ,该球与圆柱的上、下底面及母线均相切.记圆柱 $O_1 O_2$的体积为 $V_1$ ,球 $O$ 的体积为 $V_2$ ,则 $\frac{V_1}{V_2}$ 的值是
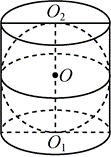
己知正三棱锥的高为 1 ,底面边长为 $2 \sqrt{3}$ ,内有一个球与四个面都相切,则该正三棱锥的内切球的半径为