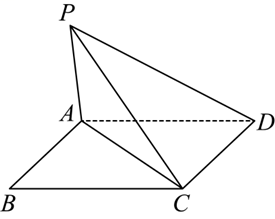
已知菱形 $A B C D$ 的各边长为 $2, \angle B=60^{\circ}$ .将 $ A B C$ 沿 $A C$ 折起,折起后记点 $B$ 为 $P$ ,连接 $P D$ ,得到三棱锥 $P-A C D$ ,如图所示,当三棱锥 $P-A C D$ 的表面积最大时,三棱锥 $P-A C D$ 的外接球体积为
A
$\frac{5 \sqrt{2}}{3} \pi$
B
$\frac{4 \sqrt{3}}{3} \pi$
C
$2 \sqrt{3} \pi$
D
$\frac{8 \sqrt{2}}{3} \pi$
E
F