填空题 (共 9 题 ),请把答案直接填写在答题纸上
若 $(a-3)^2+\sqrt{b-5}=0$ ,则以 $a, ~ b$ 为边长的等腰三角形的周长为
等边三角形 $A B C$ 中,$D$ 是边 $B C$ 上的一点,$B D=2 C D$ ,以 $A D$ 为边作等边三角形 $A D E$ ,连接 $C E$ .若 $C E=2$ ,则等边三角形 $A B C$ 的边长为
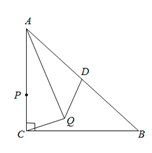
在 $Rt \triangle A B C$ 中,$\angle C=90^{\circ}$ ,有一个锐角为 $60^{\circ}, A B=6$ ,若点 $P$ 在直线 $A B$ 上(不与点 $A , B$ 重合),且 $\angle P C B=30^{\circ}$ ,则 $A P$ 的长为
如图,在 $\triangle A B C$ 中,$\angle A B C=40^{\circ}, \angle B A C=80^{\circ}$ ,以点 A 为圆心,$A C$ 长为半径作弧,交射线 $B A$ 于点 $D$ ,连接 $C D$ ,则 $\angle B C D$ 的度数是
矩形 $A B C D$ 中,$A B=8, A D=7$ ,点 $E$ 在 $A B$ 边上,$A E=5$ .若点 $P$ 是矩形 $A B C D$ 边上一点,且与点 $A, E$构成以 $A E$ 为腰的等腰三角形,则等腰三角形 $A E P$ 的底边长是
已知点 $A$ 在反比例函数 $y=\frac{12}{x}(x>0)$ 的图象上,点 $B$ 在 $x$ 轴正半轴上,若 $ O A B$ 为等腰三角形,且腰长为5,则 $A B$ 的长为
在 $\triangle A B C$ 中,$A D$ 为边 $B C$ 上的高,$\angle A B C=30^{\circ}, \angle C A D=20^{\circ}$ ,则 $\angle B A C$ 是 $\qquad$度。
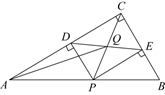
如图,在Rt $\triangle A B C$ 中,$\angle A C B=90^{\circ}, \angle B=60^{\circ}, B C=2$ ,点 $P$ 为斜边 $A B$ 上的一个动点(点 $P$ 不与点 $A . B$重合),过点 $P$ 作 $P D \perp A C, P E \perp B C$ ,垂足分别为点 $D$ 和点 $E$ ,连接 $D E, P C$ 交于点 $Q$ ,连接 $A Q$ ,当 $\triangle A P Q$为直角三角形时,$A P$ 的长是 $\qquad$
如图,在 Rt $\triangle A B C$ 中,$\angle A C B=90^{\circ}, A C=B C=2 \sqrt{2}$ ,点 $D$ 为 $A B$ 的中点,点 $P$ 在 $A C$ 上,且 $C P=1$ ,将 $C P$ 绕点 $C$ 在平面内旋转,点 $P$ 的对应点为点 $Q$ ,连接 $A Q, D Q$ .当 $\angle A D Q=90^{\circ}$ 时,$A Q$ 的长为 $\qquad$