单选题 (共 6 题 ),每题只有一个选项正确
图中p是一圆的竖直直径pc的上端点,一质点从p开始分别沿不同的弦无摩擦下滑时,到达各弦的下端所用的时间相比较是
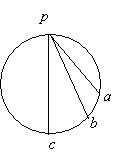
$\text{A.}$ 到a用的时间最短
$\text{B.}$ 到b用的时间最短
$\text{C.}$ 到c用的时间最短
$\text{D.}$ 所用时间都一样
质点作半径为R的变速圆周运动时的加速度大小为(v表示任一时刻质点的速率)
$\text{A.}$ $\frac{d t}{d t}$.
$\text{B.}$ $\frac{v^2}{R}$.
$\text{C.}$ $\frac{\mathrm{d} v}{\mathrm{~d} t}+\frac{v^2}{R}$.
$\text{D.}$ $\left[\left(\frac{d y}{d t}\right)^2+\left(\frac{y^4}{R^2}\right)\right]^{1 / 2}$
一运动质点在某瞬时位于矢径 $\vec{r}(x, y)$ 的端点处, 其速度大小为
$\text{A.}$ $\frac{d r}{d t}$
$\text{B.}$ $\frac{d \vec{r}}{d t}$
$\text{C.}$ $\frac{d|\vec{r}|}{d t}$
$\text{D.}$ $\sqrt{\left(\frac{d x}{d t}\right)^2+\left(\frac{d y}{d t}\right)^2}$
以下五种运动形式中, $\vec{a}$ 保持不变的运动是
$\text{A.}$ 单摆的运动.
$\text{B.}$ 匀速率圆周运动.
$\text{C.}$ 行星的椭圆轨道运动.
$\text{D.}$ 抛体运动.
$\text{E.}$ 圆锥摆运动.
一物体从某一确定高度以 ${v_0}$ 的速度水平抛出, 已知它落地时的速度为 ${v_t}$, 那么它运动的时间是
$\text{A.}$ $\frac{y_t-y_0}{g}$.
$\text{B.}$ $\frac{y_t-y_0}{2 g}$.
$\text{C.}$ $\left(v_t^2-v_0^2\right)^{1 / 2}$
$\text{D.}$ $\frac{\left(v_t^2-y_0^2\right)^{1 / 2}}{2 g}$
将细绳绕在一个具有水平光滑轴的飞轮边缘上, 现在在绳端挂一质量为 $\mathrm{m}$ 的重物, 飞轮的角加速度为 $\beta$. 如果以拉 力 $2 \mathrm{mg}$ 代替重物拉绳时, 飞轮的角加速度将
$\text{A.}$ 小于 $\beta$
$\text{B.}$ 大于 $\beta$, 小于 $2 \beta$
$\text{C.}$ 大于 $2 \beta$
$\text{D.}$ 等于 $2 \beta$