单选题 (共 2 题 ),每题只有一个选项正确
若随机变量 $X \sim N(6,1)$ ,且 $P(5 < X \leq 7)=a, P(4 < X \leq 8)=b$ ,则 $P(4 < X \leq 7)$ 等于
$\text{A.}$ $\frac{b-a}{2}$
$\text{B.}$ $\frac{b+a}{2}$
$\text{C.}$ $\frac{1-b}{2}$
$\text{D.}$ $\frac{1-a}{2}$
离散型随机变量 $X$ 的分布列如下:
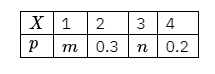
若 $E(X)=2.7$ ,则下列结论错误的是
$\text{A.}$ $m+n=0.5$
$\text{B.}$ $E(3 X-1)=7.1$
$\text{C.}$ $D(X)=0.81$
$\text{D.}$ $P(X>2)=0.5$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
随着"双十一购物节"的来临,某服装店准备了抽奖活动回馈新老客户,活动规则如下:奖券共 3 张,分别可以再店内无门槛优惠 10 元, 20 元和 30 元,每人每天可抽 1 张奖券,每人抽完后将所抽取奖券放回,以供下一位顾客抽取.若某天抽奖金额少于 20 元,则下一天可无放回地抽 2 张奖券,以优惠金额更大的作为所得,否则正常抽取.
(1)求第二天获得优惠金额的数学期望;
(2)记"第 $i$ 天抽取 1 张奖券"的概率为 $P_i$ ,写出 $P_i$ 与 $P_{i+1}$ 的关系式并求出 $P_i$ .
甲同学计划去参观某景点,但门票需在网上预约.该同学从第一天开始,每天在规定的预约时间段开始预约,若预约成功,便停止预约;若连续预约三天都没成功,则放弃预约.假设该同学每天预约门票成功的概率均为 0.7 ,
(1)求甲同学到第三天才预约成功的概率;
(2)记 $X$ 为甲同学预约门票的天数,求 $X$ 的分布列和期望 $E(X)$ .
第 19 届亚运会于 2023 年 9 月 23 日至 10月 8 日在杭州举行,为弘扬奥林匹克和亚运精神,增强锻炼身体意识,某学校举办一场羽毛球比赛。已知羽毛球比赛的单打规则是:若发球方胜,则发球方得 1 分,且继续在下一回合发球;若接球方胜,则接球方得 1分,且成为下一回合发球方。现甲,乙二人进行羽毛球单打比赛,根据以往甲,乙两名运动员对阵的比赛数据可知,若甲发球,甲得分的概率为 $\frac{3}{5}$ ,乙得分的概率为 $\frac{2}{5}$ ;若乙发球,乙得分的概率为 $\frac{4}{5}$ ,甲得分的概率为 $\frac{1}{5}$ .规定第 1 回合是甲先发球。
(1)求第 3 回合由甲发球的概率;
(2) ① 设第 i 回合是甲发球的概率为 $p_i$ ,证明:$\left\{p_i-\frac{1}{3}\right\}$ 是等比数列;
② 已知:若随机变量 $X_i$ 服从两点分布,且 $P\left(X_i=1\right)=1-P\left(X_i=0\right)=q_i, i =1,2, \cdots, n$ ,则 $E\left(\sum_{i=1}^n X_i\right)=$ $\sum_{i=1}^n q_i$ .若第 1 回合是甲先发球,求甲,乙连续进行 $n$ 个回合比赛后,甲的总得分的期望.
甲口袋中装有 2 个黑球和 1 个白球,乙口袋中装有 1 个黑球和 2 个白球。现从甲,乙两口袋中各任取一个球交换放入另一口袋,称为 1 次球交换的操作,重复 $n$ 次这样的操作,记甲口袋中黑球个数为 $X_n$ .
(1)求 $X_2$ 的概率分布列并求 $E\left(X_2\right)$ ;
(2)求证:$\left\{E\left(X_n\right)-\frac{3}{2}\right\}\left(n \geqslant 2\right.$ 且 $\left.n \in N^*\right)$ 为等比数列,并求出 $E\left(X_n\right)\left(n \geqslant 2\right.$ 且 $\left.n \in N^*\right)$ .