单选题 (共 3 题 ),每题只有一个选项正确
已知三棱锥 P−ABC 的四个顶点在球 O 的球面上,PA=PB=PC,△ABC 是边长为 2 的正三角形,E,F 分别是 PA,AB 的中点,∠CEF=90°,则球 O 的体积为
$\text{A.}$ $8 \sqrt{6} \pi$
$\text{B.}$ $4 \sqrt{6} \pi$
$\text{C.}$ $2 \sqrt{6} \pi$
$\text{D.}$ $ \sqrt{6} \pi$
如图, 已知长方体 $A B C D-A_1 B_1 C_1 D_1$ 的体积为 $16, A B=$ $2 A A_1=2 B C, A D_1$ 与 $A_1 D$ 相交于点 $E$, 则三棱锥 $E-A C D$ 的外接球的表面积为
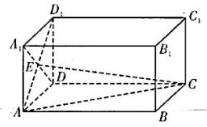
$\text{A.}$ $12 \pi$
$\text{B.}$ $16 \pi$
$\text{C.}$ $20 \pi$
$\text{D.}$ $36 \pi$
已知球 $O$ 的直径 $|P Q|=4, A, B, C$ 是球 $O$ 球面上的三点, $\triangle A B C$ 是等边三角形, 且 $\angle A P Q=\angle B P Q=\angle C P Q=30^{\circ}$, 则三棱椎 $P-A B C$ 的体积为
$\text{A.}$ $\frac{9 \sqrt{3}}{4}$
$\text{B.}$ $\frac{27 \sqrt{3}}{4}$
$\text{C.}$ $\frac{3 \sqrt{3}}{2}$
$\text{D.}$ $\frac{3 \sqrt{3}}{4}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
在三椶钪 $P-A B C$ 中,三条棱 $P A, P B, P C$ 两两韭直, 且 $P A=P B=P C=2$, 则平面 $A B C$ 截该三棱锥 的外接球所得截面因的面积为
已知一个正三棱柱既有内切球又有外接球, 且外接球的表面积为 $40 \pi$, 则该三棱柱的体积为