解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图,直四棱柱$ ABCD–A_1B_1C_1D_1 $的底面是菱形, $AA_1=4 , AB=2 , ∠ BAD=60°, E, M, N $ 分别是
$BC,BB_1,A_1D$ 的中点.

(1)证明:$MN$∥平面 $C_1DE$;
(2)求二面角 $A−MA_1−N$ 的正弦值
如图, 在直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 中, $A C \perp B C, A C=B C=2, C C_{1}=3$, 点 $D, E$ 分别在棱 $A A_{1}$ 和棱 $C C_{1}$ 上, 且 $A D=1, C E=2$.
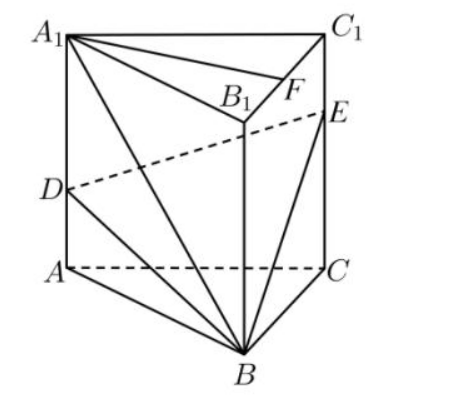
(1) 设 $F$ 为 $B_{1} C_{1}$ 中点, 求证: $A_{1} F / /$ 平面 $B D E$;
(2) 求直线 $A_{1} B_{1}$ 与平面 $B D E$ 所成角的正弦值.
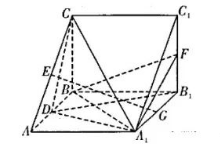
如图, 在直三棱柱 $A B C-A_1 B_1 C_1$ 中, $A B \perp B C$, 侧面 $A B B_1 A_1$ 为正方形, 点 $D, E, F, G$ 分别为棱 $A B, A C, B_1 C_1, A_1 B_1$ 的中点.
(1)求证: $G E / /$ 平面 $B C C_1 B_1$;
(2) 若二面角 $B_1-A_1 D-C$ 的余弦值为 $\frac{\sqrt{21}}{21}$, 且 $A B=2$, 求多面体 $A B C A_1 F C_1$ 的体积.
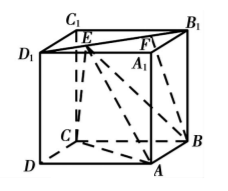
如图, 正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $1, E, F$ 是线段 $B_1 D_1$ 上的两个动点.
(1) 若 $B F / /$ 平面 $A C E$, 求 $E F$ 的长度;
(2) 若 $\overrightarrow{D_1 E}=\frac{1}{4} \overrightarrow{D_1 B_1}$, 求直线 $B E$ 与平面 $A C E$ 所成角的正弦值.
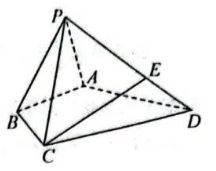
如图, 在三棱雉 $P-A B C$ 中, $A B \perp B C, A B=2, B C=2 \sqrt{2}, P B=P C=\sqrt{6}$, $B P, A P, B C$ 的中点分别为 $D, E, O, A D=\sqrt{5} D O$, 点 $F$ 在 $A C$ 上, $B F \perp A O$.
(1) 证明: $E F / /$ 平面 $A D O$;
(2) 证明: 平面 $A D O \perp$ 平面 $B E F$;
(3) 求二面角 $D-A O-C$ 的正弦值.
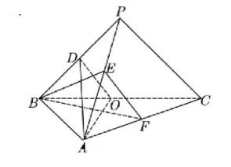
如图, 在四棱锥 $P-A B C D$ 中, 底面四边形 $A B C D$ 满足 $A B=C B=\sqrt{2}, A D=C D=\sqrt{5}$, $\angle A B C=90^{\circ}$, 棱 $P D$ 上的点 $E$ 满足 $P E=2 D E$.
(1) 证明: 直线 $C E / /$ 平面 $P A B$;
(2) 若 $P B=\sqrt{5}, P D=2 \sqrt{2}$, 且 $P A=P C$, 求直线 $C E$ 与平面 $P B C$ 所成角的正弦值.