单选题 (共 6 题 ),每题只有一个选项正确
若 $f(x)=\left\{\begin{array}{cc}\frac{1-\cos \sqrt{x}}{a x}, & x>0 \\ b, & x \leq 0\end{array}\right.$ 在 $x=0$ 处连续, 则
$\text{A.}$ $a b=\frac{1}{2}$
$\text{B.}$ $a b=-\frac{1}{2}$
$\text{C.}$ $a b=0$
$\text{D.}$ $a b=2$
设二阶可导函数 $f(x)$ 满足 $f(1)=f(-1)=1, f(0)=-1$且 $f^{\prime \prime}(x)>0$ ,则
$\text{A.}$ $\int_{-1}^1 f(x) \mathrm{d} x>0$
$\text{B.}$ $\int_{-1}^1 f(x) \mathrm{d} x < 0$
$\text{C.}$ $\int_{-1}^0 f(x) \mathrm{d} x>\int_0^1 f(x) \mathrm{d} x$
$\text{D.}$ $\int_{-1}^0 f(x) \mathrm{d} x < \int_0^1 f(x) \mathrm{d} x$
设数列 $\left\{x_n\right\}$ 收敛,则
$\text{A.}$ 当 $\lim _{n \rightarrow \infty} \sin x_n=0$ 时, $\lim _{n \rightarrow \infty} x_n=0$
$\text{B.}$ 当 $\lim _{n \rightarrow \infty}\left(x_n+\sqrt{\left|x_n\right|}\right)=0$ 时,则 $\lim _{n \rightarrow \infty} x_n=0$
$\text{C.}$ 当 $\lim _{n \rightarrow \infty}\left(x_n+x_n^2\right)=0$ 时,则 $\lim _{n \rightarrow \infty} x_n=0$
$\text{D.}$ 当 $\lim _{n \rightarrow \infty}\left(x_n+\sin x_n\right)=0$ 时,则 $\lim _{n \rightarrow \infty} x_n=0$
微分方程 $y^{\prime \prime}-4 y^{\prime}+8 y=e^{2 x}(1+\cos 2 x)$ 的特解可设为 $y^*=(\quad)$
$\text{A.}$ $A e^{2 x}+e^{2 x}(B \cos 2 x+C \sin 2 x)$
$\text{B.}$ $A x e^{2 x}+e^{2 x}(B \cos 2 x+C \sin 2 x)$
$\text{C.}$ $A e^{2 x}+x e^{2 x}(B \cos 2 x+C \sin 2 x)$
$\text{D.}$ $A x e^{2 x}+x e^{2 x}(B \cos 2 x+C \sin 2 x)$
设 $f(x, y)$ 具有一阶偏导数,且在任意的 $(x, y)$ 都有 $\frac{\partial f(x, y)}{\partial x}>0, \frac{\partial f(x, y)}{\partial y} < 0$ ,则
$\text{A.}$ $f(0,0)>f(1,1)$
$\text{B.}$ $f(0,0) < f(1,1)$
$\text{C.}$ $f(0,1)>f(1,0)$
$\text{D.}$ $f(0,1) < f(1,0)$
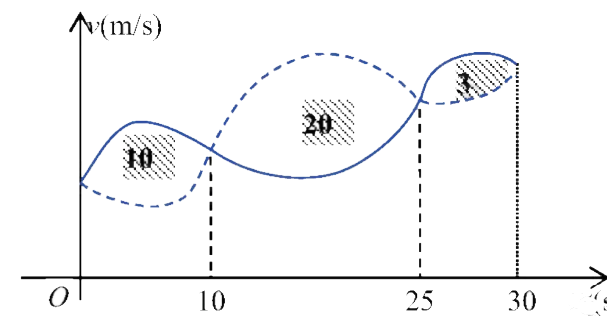
甲乙两人赛跑,计时开始时,甲在乙前方 10 (单位:m) 处.图中,实线表示甲的速度曲线 $v=v_1(t)$ (单位: $\mathrm{m} / \mathrm{s}$ )虚线表示乙的速度曲线 $v=v_2(t)$ ,三块阴影部分面积的数值依次为 $10 , 20 , 3$ ,计时开始后乙追上甲的时刻记为 $t_0$ (单位: $s$ ),则
$\text{A.}$ $t_0=10$
$\text{B.}$ $15 < t_0 < 20$
$\text{C.}$ $t_0=25$
$\text{D.}$ $t_0>25$