一、单选题 （共 11 题，每小题 5 分，共 50 分，每题只有一个选项正确）
设随机变量 $X$ 的分布函数为 $F_X(x)=\left\{\begin{array}{l}0, x < 3 \\ 0.8,3 \leqslant x < 5 \\ 1, x \geqslant 5\end{array}\right.$, 随机变量 $Y$ 的分布函数为 $F_Y(x)= \left\{\begin{array}{l}
0, x < 5 \\
0.2,5 \leqslant x < 7 \\
1, x \geqslant 7
\end{array}\right.$ 下列说法正确的是
$\text{A.}$ $P(X+Y=10)=0.68$
$\text{B.}$ 若 $X$ 与 $Y$ 不相关, 则 $X$ 与 $Y$ 独立
$\text{C.}$ $X+Y=10$
$\text{D.}$ $P(X=3, Y=7)=0.64$
设总体 $X$ 的概率分布如下
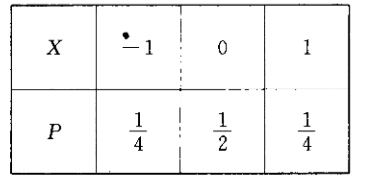
从总体中抽取 $n$ 个简单随机样本, $N_1$ 表示 $n$ 个样本中取到 -1 的个数, $N_2$ 表示 $n$ 个样本中取 到 0 的个数, $N_3$ 表示 $n$ 个样本中取到 1 的个数, 则 $N_1$ 与 $N_2$ 的相关系数为
$\text{A.}$ $-\frac{\sqrt{3}}{3}$.
$\text{B.}$ $\frac{\sqrt{3}}{3}$.
$\text{C.}$ $-1$
$\text{D.}$ $1$
设 $X_1, X_2, X_3, X_4$ 为从正态总体 $N\left(0, \sigma^2\right)$ 中抽取的一个简单随机样本, $\bar{X}$ 为样本均值, $S^2$ 为样本方差, 令统计量 $T=\frac{2 \bar{X}}{S}$, 若 $P(T < -1)=0.15$, 则 $P(0 < T < 1)= $.
$\text{A.}$ 0.15
$\text{B.}$ 0.25
$\text{C.}$ 0.35
$\text{D.}$ 0.45
设总体 $X$ 的密度函数为
$$
f(x)= \begin{cases}\sqrt{\theta} x^{\sqrt{\theta}-1}, & 0 \leqslant x \leqslant 1, \\ 0, & \text { 其他, }\end{cases}
$$
$x_1, x_2, \cdots, x_n$ 为总体 $X$ 的一组样本观测值, 则末知参数 $\theta$ 的极大似然估计值 $\hat{\theta}$ 为
$\text{A.}$ $\frac{n}{\left(\sum_{i=1}^n \ln x_i\right)^2}$
$\text{B.}$ $\frac{n^2}{\left(\sum_{i=1}^n \ln x_i\right)^2}$
$\text{C.}$ $\frac{n^2}{\sum_{i=1}^n \ln x_i}$
$\text{D.}$ $\frac{n}{\sum_{i=1}^n \ln x_i}$
设 $X_1 \sim N(1,1), X_2 \sim N(2,4)$, 又 $X_3 \sim\left(\begin{array}{cc}0 & 1 \\ \frac{1}{3} & \frac{2}{3}\end{array}\right)$, 且 $X_1, X_2, X_3$ 相互独立, $Z=\left(X_1-1\right) X_3+\left(X_2-2\right)\left(1-X_3\right)$, 则 $P\{Z \geqslant 0\}=$.
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
将长度为 $1 \mathrm{~m}$ 的木棒随机地截成两段, 设第一段长度的 $\frac{1}{5}$ 为 $X$, 第二段长度的 $\frac{1}{7}$ 为 $Y$, 则 $X, Y$的相关系数 $\rho_{X Y}=$
$\text{A.}$ -1 .
$\text{B.}$ $-\frac{1}{35}$.
$\text{C.}$ $\frac{1}{35}$.
$\text{D.}$ 1
假设总体 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right), X_1, \cdots, X_n$ 是来自总体 $X$ 的简单随机样本, 其样本均值为 $\bar{X}$, 如果 $P\{|X-\mu| < a\}=P\{|\bar{X}-\mu| < b\}$, 其中 $\sigma>0$, 则有
$\text{A.}$ $a=n b$.
$\text{B.}$ $b=n a$.
$\text{C.}$ $a=\sqrt{n} b$.
$\text{D.}$ $b=\sqrt{n} a$.
设平面区域 $D=\left\{(x, y) \mid 0 \leqslant x \leqslant 2,0 \leqslant y \leqslant 4-x^2\right\}$, 在 $D$ 上随机取一点 $(X, Y)$, 令随机变量 $U=\left\{\begin{array}{ll}0, & X \leqslant 1, \\ 1, & X>1,\end{array} \quad V=\left\{\begin{array}{cc}-1, & Y \leqslant 3, \\ 1, & Y>3,\end{array}\right.\right.$ 则 $U$ 和 $V$ 的相关系数 $\rho_{U V}=(\quad)$.
$\text{A.}$ $\sqrt{\frac{5}{77}}$
$\text{B.}$ $-\sqrt{\frac{5}{77}}$
$\text{C.}$ $\frac{5}{\sqrt{77}}$
$\text{D.}$ $-\frac{5}{\sqrt{77}}$
设二维随机变量 $(X, Y)$ 的分布律
则 $P\{X+Y \leq 1\}=$
$\text{A.}$ 0.4
$\text{B.}$ 0.3
$\text{C.}$ 0.2
$\text{D.}$ 0.1
设随机变量 $X_1, X_2, \cdots, X_{100}$ 独立同分布, $E\left(X_i\right)=0, D\left(X_1\right)=1, i=1,2, \cdots, 100$,则由中心极限定理得 $P\left\{\sum_{i=1}^{100} X_i \leq 10\right\}$ 近似于
$\text{A.}$ 0
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $\Phi(10)$
$\text{D.}$ $\Phi(100)$
设总体 $X \sim N(\mu, 1), Y \sim N(\mu, 1)$, 且 $X, Y$ 相互独立, $X_1, X_2, \cdots, X_n$ 与 $Y_1, Y_2, \cdots, Y_n$ 分别来自总体 $X, Y$ 的简单随机样本, 设 $X=\frac{1}{n} \sum_{i=1}^n X_i, Y=\frac{1}{n} \sum_{i=1}^n Y_i, S_X^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2$, $S_Y^2=\frac{1}{n-1} \sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2$, 则 $\frac{\sqrt{n}(\bar{X}-\bar{Y})}{\sqrt{S_X^2+S_Y^2}}$ 服从
$\text{A.}$ $t(n-1)$
$\text{B.}$ $t(n)$
$\text{C.}$ $t(2 n)$
$\text{D.}$ $t(2 n-2)$
二、填空题 （共 16 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
设 $X \sim B(2, p), Y \sim B(3, p)$, 且 $P\{X \geq 1\}=\frac{5}{9}$, 则 $P\{Y \geq 1\}=$
设连续型随机变量 $X$ 的密度函数为 $f(x)=\frac{1}{\sqrt{\pi}} e^{-x^2+2 x-1} \quad(-\infty < x < +\infty)$, 求 $E(X)$ 与 $D(X)$.
设随机变量 $X$ 服从区间 $(0,2)$ 上的均匀分布, 求 $\frac{D(X)}{E\left(X^2\right)}$
设 $X \sim E(\lambda), Y \sim E(\lambda)$ 且 $X, Y$ 相互独立, $Z=\min \{X, Y\}$, 则 $P\{Z>E(Z)\}=$
设连续函数 $f(x)$ 非负, 且 $f(x) \int_0^1 f(t x) \mathrm{d} t=2 x^2$, 则 $f(x)$ 在区间 $[0,2]$ 上的平均值为
市场上某产品由甲、乙两厂生产. 已知甲厂和乙厂的产品指标服从分布函数 $F_1(x)$ 和 $F_2(x)$,且甲厂的产量是乙厂的 3 倍, 则从市场上任取一件产品, 其指标服从的分布函数为
设随机变量 $X \sim N(0,1), Y \sim N(0,4)$, 且 $X$ 与 $Y$ 相互独立, 又 $F \sim F\left(n_1, n_2\right)$, 记 $\mathrm{P}\left\{F>F_\alpha\left(n_1, n_2\right)\right\}=\alpha(0 < \alpha < 1)$, 若 $\mathrm{P}\left\{\frac{|X|}{|Y|} \leqslant b\right\}=0.9$, 则 $b=$ . (用分位点 $F_\alpha\left(n_1, n_2\right)$ 表示)
设二维随机变量 $(X, Y)$ 的分布律为
则 $P\{Y=2\}=$
设随机变量 $X \sim N(1,4)$, 则 $D(X)=$
设二维随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
c x, & 0 < x < 1, \quad 0 < y < 1, \\
0, & \text { 其他, }
\end{array}\right.
$$
(1)求常数 $c$;
(2) 求 $(X, Y)$ 分别关于 $X, Y$ 的边缘摡率密度;
(3) 试问 $X$ 与 $Y$ 是否相互独立, 为什么?
设随机变量$X$的分布律为
记$ Y=X^2$,
求 (1)$ D(X), D(Y)$ (2)$\operatorname{Cov}(X, Y)$
设二维随机变量 $(X, Y)$ 服从正态分布 $N(-1,2 ; 2,2 ; \rho)$, 若 $X+Y$ 与 $X-2 Y$ 相互独立, 则 $\rho=$
已知二维随机变量 $(X, Y)$ 的联合分布律: 要使 $X 、 Y$ 相互独立, 则 $\alpha, \beta$ 的值为
加油站有两套用来加油的设备, 设备 $A$ 是工作人员操作的, 设备 $B$ 是顾客自己操作的, $A 、 B$ 均装有两根加油软管, 任取一时间, $A 、 B$ 正在使用的软管数分别为 $X 、 Y, X 、 Y$ 的联合分布律为下表，求:
(1) $P(X \leq 1, Y \leq 1)$
(2) 至少有一根软管在使用的概率
(3) $P(X=Y)$
(4) $P\{X+Y=2\}$
设 $A 、 B$ 为两个随机事件, $P\{A\}=0.25, P\{B \mid A\}=0.5, P\{A \mid B\}=0.25$, 令随机变量
$$
X=\left\{\begin{array}{rrr}
1 & A \text { 发生 } \\
0 & A \text { 不发生 }
\end{array} \quad Y=\left\{\begin{array}{rr}
1 & B \text { 发生 } \\
0 & B \text { 不发生 }
\end{array}\right.\right.
$$
(1) 求 $(X, Y)$ 的联合分布律
(2) 求 $P\left\{X^2+Y^2=1\right\}$
将编号为 $1,2,3$ 的三个球随机放入编号为 $1,2,3$ 的三个盒子中，每盒仅放一个球，令
$$
X_i=\left\{\begin{array}{ll}
1, & \text { 第 } i \text { 号球放第 } i \text { 号盒中, } \\
0, & \text { 其他 }
\end{array}(i=1,2),\right.
$$
则 $\rho_{X_1 X_2}=$
三、解答题 （ 共 11 题，满分 80 分，解答过程应写出必要的文字说明、证明过程或演算步骤 ）
设连续型随机变量 $X$ 的分布函数为
$$
F(x)=A+B \arctan x \quad(-\infty < x < +\infty)
$$
试求: (1). 系数 $A$ 与 $B$; (2). 概率 $P\{-1 < X < 1\} ;$ (3). 随机变量 $X$ 的密度函数.
设随机变量 $X \sim N(0,1), Y=X^2+1$, 试求随机变量 $Y$ 的密度函数.
设二维连续型随机变皇 $(X, Y)$ 的概率密度函数为
$$
f(x, y)=\left\{\begin{array}{cc}
C e^{-2 x}, & x>0,0 < y < x, \\
0, & \text { 其它. }
\end{array}\right.
$$
1. 确定常数 $C$ 的值;
2. 求 $X$ 与 $Y$ 边缘概率密度函数 $f_X(x)$ 和 $f_Y(y)$, 并判断 $X$ 与 $Y$ 是否独立;
3. 求 $Z=X+Y$ 的概率密度函数 $\mathrm{f}_{\mathrm{Z}}(z)$;
4. 求概率 $P(X \leq Y+2)$.
设随机向量 $(\xi, \eta)$ 服从区域 $D$ 上的均匀分布, 其中 $D$ 是由直线 $y=x, x=0, y=$ 1所围成的区域. 试求:
(1) $(\xi, \eta)$ 的联合密度 $p(x, y)$;
(2) $(\xi, \eta)$ 的边缘密度 $p_1(x)$ 和 $p_2(y)$;
(3) 条件密度 $p(x \mid \eta=y)$;
(4) $E(\xi \mid \eta=y)$.
设随机变量 $X, Y$ 和 $Z$ 相互独立, 且均服从参数为 1 的指数分布. 记
$$
U=\frac{X}{X+Y}, \quad V=\frac{X+Y}{X+Y+Z}, \quad W=X+Y+Z .
$$
(1) 计算随机向量 $(U, V, W)$ 的联合密度函数.
(2) 随机变量 $U, V$ 和 $W$ 是否相互独立? 请证明你的结论.
设随机变量 $X$ 服从参数为 2 的指数分布。
证明: $\bar{Y}=1-e^{-2 X}$ 在区间 $(0,1)$ 上, 服从均匀分布。
设区域 $D=\{(x, y) \mid 0 \leqslant x \leqslant \sqrt{y}, 0 \leqslant y \leqslant 1\}$, 二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)= \begin{cases}6 x y, & (x, y) \in D, \\ 0, & \text { 其他. }\end{cases}
$$
(I) 判断 $X, Y$ 是否相互独立;
(II) 求 $Z=\sqrt{X^2+Y}$ 的分布函数.
设总体 $(X, Y)$ 的分布函数为
$$
F(x, y)= \begin{cases}0, & x < 0 \text { 或 } y < \theta, \\ p\left[1-\mathrm{e}^{-(y-\theta)}\right], & 0 \leqslant x < 1, y \geqslant \theta, \\ 1-\mathrm{e}^{-(y-\theta)}, & x \geqslant 1, y \geqslant \theta .\end{cases}
$$
其中 $p, \theta$ 为末知参数, 且 $0 < p < 1$.
(I) 求 $X$ 的概率分布和 $Y$ 的概率密度, 并判别 $X$ 和 $Y$ 的独立性;
(II) 求 $Z=X+Y$ 的概率密度 $f_Z(z)$.
已知编号为 1 的盒子中装有 2 个白球和 1 个红球, 编号为 2 的盒子中装有 3 个白球, 现随机各取一球, 交换放人另一个盒子中, 交换两次, 记 $X$ 为红球所在盒子的编号, $Y$ 服从参数为 1 的指数分布, 随机变量 $X$ 与 $Y$ 相互独立, 令 $Z=\frac{Y}{X}$.
(I) 求 $Z$ 的概率密度;
( II) $Y$ 与 $Z$ 是否相互独立?
设随机变量 $X$ 和 $Y$ 独立同分布, 且
$$
X \sim f(x)=\left\{\begin{array}{cc}
\frac{\sqrt{2}}{\sqrt{\pi}} \mathrm{e}^{-\frac{x^2}{2}}, & x>0, \\
0, & x \leqslant 0 .
\end{array} \text { 且 } Z=\frac{\min \{X, Y\}}{\max \{X, Y\} .}\right.
$$
(I) 求 $Z$ 的概率密度函数;
(II) 判断 $X$ 和 $Z$ 的独立性, 并说明理由.
设二维随机变量 $(X, Y)$ 在区域 $D=\{(x, y)|| x+y|\leqslant 1| x-y \mid, \leqslant 1\}$ 上服从均匀分布, 求:
$(I)(X, Y)$ 的边缘概率密度 $f_X(x), f_Y(y)$;
(II) $Z=X+Y$ 的概率密度 $f_Z(z)$;
(III) $P\left\{\left.|Y| \leqslant \frac{1}{2}|| X \right\rvert\, \leqslant \frac{1}{2}\right\}$.