一、单选题 （共 43 题，每小题 5 分，共 50 分，每题只有一个选项正确）
用激光笔照射透明塑料制成的光盘边缘时观察到的现象如图所示。入射点O和两出射点P、Q恰好位于光盘边缘等间隔的三点处，空气中的四条细光束分别为入射光束a、反射光束b、出射光束c和d、已知光束a和b间的夹角为 $90^{\circ}$，则
$\text{A.}$ 光盘材料的折射率 2
$\text{B.}$ 光在光盘内的速度为真空中光速的三分之二
$\text{C.}$ 光束b、c和d的强度之和等于光束a的强度
$\text{D.}$ 光束c的强度小于O点处折射光束 的强度
“测温枪”(学名“红外线辐射测温仪”)具有响应快、非接触和操作方便等优点。它是根据黑体辐射规律设计出来的，能将接收到的人体热辐射转换成温度显示。若人体温度升高，则人体热辐射强度I及其极大值对应的波长 $\lambda$ 的变化情况是
$\text{A.}$ $I$ 增大, $\lambda$ 增大
$\text{B.}$ $I$ 增大, $\lambda$ 减小
$\text{C.}$ $I$ 减小, $\lambda$ 增大
$\text{D.}$ $I$ 诚小, $\lambda$ 减小
在抗击新冠病毒的过程中，广泛使用了红外体温计测量体温，如图所示。下列说法正确的是
$\text{A.}$ 当体温超过37.3℃时人体才辐射红外线
$\text{B.}$ 当体温超过周围空气温度时人体才辐射红外线
$\text{C.}$ 红外体温计是依据体温计发射红外线来测体温的
$\text{D.}$ 红外体温计是依据人体温度越高，辐射的红外线强度越大来测体温的
下列说法正确的是
$\text{A.}$ 质子的德布罗意波长与其动能成正比
$\text{B.}$ 天然放射的三种射线，穿透能力最强的是a 射线
$\text{C.}$ 光电效应实验中的截止频率与入射光的频率有关
$\text{D.}$ 电子束穿过铝箔后的衍射图样说明电子具有波动性
如图所示, 圆心为 $O$ 、半径为 $R$ 的半圆形玻璃砖置于水平桌面上, 光线从 $P$ 点垂直界面入射后, 恰好在玻 璃砖圆形表面发生全反射; 当入射角 $\theta=60^{\circ}$ 时, 光线从玻璃砖圆形表面出射后恰好与入射光平行。已知真 空中的光速为 $c$, 则
$\text{A.}$ 玻璃砖的折射率为 1.5
$\text{B.}$ $O P$ 之间的距离为 $\frac{\sqrt{2}}{2} R$
$\text{C.}$ 光在玻璃砖内的传播速度为 $\frac{\sqrt{3}}{3} c$
$\text{D.}$ 光从玻璃到空气的临界角为 $30^{\circ}$
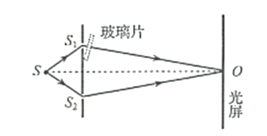
双缝干涉实验装置的截面图如图所示。光源 $\mathrm{S}$ 到 $\mathrm{S}_1 、 \mathrm{~S}_2$ 的距离相等, $O$ 点为 $\mathrm{S}_1 、 \mathrm{~S}_2$ 连线中垂线与光屏的交 点。光源 $\mathrm{S}$ 发出的波长为 $\lambda$ 的光, 经 $\mathrm{S}_1$ 出射后垂直穿过玻璃片传播到 $O$ 点, 经 $\mathrm{S}_2$ 出射后直接传播到 $O$ 点, 由 $\mathrm{S}_1$ 到 $O$ 点与由 $\mathrm{S}_2$ 到 $O$ 点, 光传播的时间差为 $\Delta t$ 。玻璃片厚度为 $10 \lambda$, 玻璃对该波长光的折射率为 1.5 , 空气中光速为 $c$, 不计光在玻璃片内的反射。以下判断正确的是
$\text{A.}$ $\Delta t=\frac{5 \lambda}{c}$
$\text{B.}$ $\Delta t=\frac{15 \lambda}{2 c}$
$\text{C.}$ $\Delta t=\frac{10 \lambda}{c}$
$\text{D.}$ $\Delta t=\frac{15 \lambda}{c}$
将一块平板玻璃放置在另一块平板玻璃上，一端夹入两张纸片，从而在两玻璃间形成一个劈形空气薄膜，光从上方入射后，从上往下看到干涉条纹如图所示。下列说法正确的是
$\text{A.}$ 若抽去一张纸片，条纹之间的距离变小
$\text{B.}$ 若把开始的紫光换成红光，条纹之间的距离变小
$\text{C.}$ 干涉条纹是两个玻璃板上表面的反射光叠加形成的
$\text{D.}$ 无论条纹是直线还是曲线，任意一条条纹所在的位置下面的空气薄膜的厚度相等
一学生小组在探究电磁感应现象时, 进行了如下比较实验。用图 (a) 所示的缠绕方式, 将漆包线分别绕 在几何尺寸相同的有机玻璃管和金属铝管上，漆包线的两端与电流传感器接通。两管皆坚直放置，将一很 小的强磁体分别从管的上端由静止释放, 在管内下落至管的下端。实验中电流传感器测得的两管上流过漆 包线的电流 $I$ 随时间 $t$ 的变化分别如图(b) 和图(c) 所示, 分析可知
$\text{A.}$ 图 (c) 是用玻璃管获得的图像
$\text{B.}$ 在铝管中下落, 小磁体做匀变速运动
$\text{C.}$ 在玻璃管中下落, 小磁体受到的电磁阻力始终保持不变
$\text{D.}$ 用铅管时测得的电流第一个峰到最后一个峰的时间间隔比用玻璃管时的短
如图, 一磁感应强度大小为 $B$ 的匀强磁场, 方向垂直于纸面 $(x O y$ 平面) 向里, 磁场右 边界与 $x$ 轴垂直。一带电粒子由 $O$ 点沿 $x$ 正向入射到磁场中, 在磁场另一侧的 $S$ 点射出, 粒子离开磁场后, 沿直线运动打在垂直于 $x$ 轴的接收屏上的 $P$ 点; $S P=l, S$ 与屏的距离 为 $\frac{l}{2}$, 与 $x$ 轴的距离为 $a$ 。如果保持所有条件不变, 在磁场区域再加上电场强度大小为 $E$ 的匀强电场, 该粒子入射后则会沿 $x$ 轴到达接收屏。该粒子的比荷为
$\text{A.}$ $\frac{E}{2 a B^2}$
$\text{B.}$ $\frac{E}{a B^2}$
$\text{C.}$ $\frac{B}{2 a E^2}$
$\text{D.}$ $\frac{B}{a E^2}$
如图所示，匀强磁场的磁感应强度为B．L形导线通以恒定电流I，放置在磁场中．已知ab边长为2l，与磁场方向垂直，bc边长为l，与磁场方向平行．该导线受到的安培力为
$\text{A.}$ 0
$\text{B.}$ BIl
$\text{C.}$ 2BIl
$\text{D.}$ $\sqrt{5}$BIl
地球表面附近空气的折射率随高度降低而增大，太阳光斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
用某种单色光进行双缝干涉实验，在屏上观察到的干涉条纹如图甲所示，改变双缝间的距离后，干涉条纹如图乙所示，图中虚线是亮纹中心的位置。则双缝间的距离变为原来的
$\text{A.}$ $\frac{1}{3}$ 倍
$\text{B.}$ $\frac{1}{2}$ 倍
$\text{C.}$ 2 倍
$\text{D.}$ 3 倍
如图所示, 圆形区域内有垂直纸面向里的匀强磁场, $O C$ 导体棒的 $O$ 端位于圆心, 棒 的中点 $A$ 位于磁场区域的边缘。现使导体棒绕 $O$ 点在纸面内逆时针转动。 $O 、 A 、 C$ 点 电势分别为 $\varphi, \varphi 、 \varphi$, 则
$\text{A.}$ $\varphi>\varphi$
$\text{B.}$ $\varphi>\varphi$
$\text{C.}$ $\varphi$
$\text{D.}$ $\varphi-\varphi-\varphi$
如图所示, 契形玻璃的横截面 $P O Q$ 的顶角为 $30^{\circ}, O P$ 边上的点光源 $S$ 到顶点 $O$ 的 距离为 $d$, 垂直于 $O P$ 边的光线 $S N$ 在 $O Q$ 边的折射角为 $45^{\circ}$ 。不考虑多次反射, $O Q$ 边 上有光射出部分的长度为
$\text{A.}$ $\frac{1}{2} d$
$\text{B.}$ $\frac{\sqrt{2}}{2} d$
$\text{C.}$ $d$
$\text{D.}$ $\sqrt{2} d$
下列光学现象, 说法正确的是
$\text{A.}$ 泊松亮斑是衍射现象, 证明了光是一种波
$\text{B.}$ “海市蜃楼” 是由于光的衍射造成的
$\text{C.}$ 两个完全相同的日光灯发出的光相遇时, 一定可以发生干涉
$\text{D.}$ 拍摄玻璃橱窗内的物品时, 往往在镜头前加装一个偏振片以增加透射光的强度
如图所示为一斜边镀银的等腰直角棱镜的截面图。一细黄光束从直角边 $A B$ 以角度 $\theta$ 入射, 依次经 $A C$ 和 $B C$ 两次反射, 从直角边 $A C$ 出射。出射光线相对于入射光线偏转了 $\alpha$ 角, 则 $\alpha$
$\text{A.}$ 等于 $90^{\circ}$
$\text{B.}$ 大于 $90^{\circ}$
$\text{C.}$ 小于 $90^{\circ}$
$\text{D.}$ 与棱镜的折射率有关
如图甲所示, 直径为 $D$ 、深度为 $H$ 的圆柱形容器内充满某种透明液体, 在其底部正中央 放置二点光源 $S$, 从液面上方看, 直径为 $d$ 的液面被光源照亮, 某物理兴趣小组想要让光 源能够照亮容器的整个液面, 在容器底部中央镶嵌二直径为 $L$ 的圆形平面镜 $M N$ (上表面 与容器底上表面齐平), 并把光源向上移动一段距离 $h$, 如图乙所示, 则
$\text{A.}$ 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{d}$
$\text{B.}$ 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{2 H}$
$\text{C.}$ 平面镜的直径 $L \geq D-d$
$\text{D.}$ 光源上移的距离 $h \geq \frac{H(D-d)}{d}$
如图所示, 边长为 $2 a$ 的正方体玻璃砖, 底面中心有一单色点光源 $O$, 从外 面看玻璃砖的上表面刚好全部被照亮，不考虑光的反射。从外面看玻璃砖 四个侧面被照亮的总面积为
$\text{A.}$ $2 a^2$
$\text{B.}$ $a^2$
$\text{C.}$ $2 \pi a^2$
$\text{D.}$ $\pi a^2$
如图所示的电源是 “恒流源”, 电源输出的电流是定值, $R$ 是光敏电阻 (光照强度增大, 电阻减小), $R_1$ 、 $R_2$ 是定值电阻, 电流表、电压表均是理想电表. 当合上开关 $\mathrm{S}$, 增大 $R$ 的光照强度, 下列说法正确的是
$\text{A.}$ 电压表的示数不变
$\text{B.}$ 电流表的示数改变
$\text{C.}$ $R_1$ 的电流减小, $R_2$ 的电压增大
$\text{D.}$ 电压表的示数与电流表的示数的乘积减小
下列各图给出了通电导体中磁感线方向或者小磁针 $\mathrm{N}$ 极指向描述正确的
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
关于电磁感应, 下列说法正确的是
$\text{A.}$ 如图 (a) 所示, 导体 $A B$ 顺着磁感线运动, 回路中有感应电流
$\text{B.}$ 如图 (b) 所示, 条形磁铁插人线圈中不动, 有感应电流产生
$\text{C.}$ 如图 (c) 所示, 开关一直接通, 小螺线管 A 插人大螺线管 B 中不动, 滑动变阻器阻值匀速滑动时无感应电流, 加速滑动时有感应电流
$\text{D.}$ 如图 (c) 所示, 开关一直接通, 小螺线管 A 插人大螺线管 B 中不动, 只要移动滑片, 电路中就有感应电流
日晕也叫圆虹, 是多出现于春夏季节的一种大气光学现象, 如图甲所示. 其原理可简化为一束太阳光射到一个截面为正六边形的冰晶上, 如图乙所示, $a 、 b$ 为其折射出的光线中的两束单色光.下列说法中正确的是
$\text{A.}$ $a$ 光光子的能量大于 $b$ 光光子的能量
$\text{B.}$ 在冰晶中 $a$ 光传播速度小于 $b$ 光传播速度
$\text{C.}$ $a 、 b$ 从冰晶射人空气发生全反射时 $b$ 光的临界角较大
$\text{D.}$ 让 $a 、 b$ 光分别通过同一双缝干涉装置, $a$ 光的相邻亮条纹间距比较大
如图甲所示是一款光电烟雾探测器的原理图. 当有烟雾进人时, 来自光源 $S$ 的光被烟雾散射后进人光电管 $C$, 光射到光电管中的钠表面时会产生光电流. 如果产生的光电流大于 $10^{-8} \mathrm{~A}$, 便会触发报警系统. 金属钠的遏止电压 $U_{\mathrm{c}}$ 随人射光频率 $\nu$ 的变化规律如图乙所示, 则
$\text{A.}$ 要使该探测器正常工作, 光源 $S$ 发出的光波频率要小于金属钠的极限频率
$\text{B.}$ 图乙中图像斜率的物理意义为普朗克常量 $h$
$\text{C.}$ 触发报警系统时钠表面会释放出光电子
$\text{D.}$ 无法通过调节光源发光的强度来调整光电烟雾探测器的灵敏度
2022 年 11 月 23 日, 我国自主研制的 16 兆瓦海上风电机组正式下线, 标志着我国海上风电技术实现重大突破. 风力发电机的工作原理可以简化为如图所示的模型: 风轮通过齿轮箱带动矩形线圈在匀强磁场中匀速转动产生交变电流, 并通过变压器和远距离输电线给灯泡 $\mathrm{L}$ 供电. 两变压器均为理想变压器, 当发电机线圈转速减小时, 下列说法中正确的是
$\text{A.}$ 通过 $R$ 的电流增加
$\text{B.}$ 降压变压器的输人电压 $U_3$ 减小
$\text{C.}$ 灯泡 L 消耗的功率增加
$\text{D.}$ 发电机的输出功率不变
有研究表明, 当兴奋情绪传播时, 在人的体表可以测出与之对应的电势变化. 某一瞬间人体表面的电势分布图如图所示, 图中实线为等差等势面, 标在等势面上的数值分别表示该等势面的电势, $a 、 b 、 c 、 d$ 为等势面上的点, 该电场可等效为两等量异种电荷产生的电场, $a 、 b$ 为两电荷连线上对称的两点, $c 、 d$ 为两电荷连线中垂线上对称的两点. 下列说法中正确的是
$\text{A.}$ $a 、 b$ 两点的电场强度不同
$\text{B.}$ $c$ 点的电势大于 $d$ 点的电势
$\text{C.}$ 将带正电的试探电荷从 $b$ 点移到 $d$ 点, 其电势能增加
$\text{D.}$ 负电荷在 $c$ 点的电势能小于在 $a$ 点的电势能
如图所示, 两光滑平行长直导轨, 间距为 $d$, 放置在水平面上, 磁感应强度为 $B$ 的匀强磁场与导轨平面垂直, 两质量都为 $m$ 、电阻都为 $r$ 的导体棒 $L_1 、 L_2$垂直放置在导轨上, 与导轨接触良好, 初始两导体棒距离足够远, $L_1$ 静止, $L_2$以初速度 $v_0$ 向右运动, 不计导轨电阻, 忽略感生电流产生的磁场, 则
$\text{A.}$ 导体棒 $L_1$ 的最终速度为 $v_0$
$\text{B.}$ 导体棒 $L_2$ 产生的焦耳热为 $\frac{3 m v_0^2}{8}$
$\text{C.}$ 通过导体棒横截面的电荷量为 $\frac{m v_0}{B d}$
$\text{D.}$ 两导体棒的初始距离最小为 $\frac{m v_0 r}{B^2 d^2}$
在物理学发展的历程中, 许多科学家的科学研究为物理学的建立做出了巨大贡献。下列叙述中正确的是
$\text{A.}$ 松香在熔化过程中温度保持不变, 松香分子的平均动能会变大
$\text{B.}$ 2023 年的诺贝尔物理学奖授予 “采用实验方法产生阿秒脉冲光的技术”, 阿秒脉冲光是一种非常短的光脉冲, 其持续时间在阿秒的量级, 即 $10^{-18} \mathrm{~s}$, 阿秒对应的物理量不是国际单位制的基本量
$\text{C.}$ 法拉第提出了电场的观点, 其实电场以及磁场是一种客观存在, 变化的电磁场和分子、原子组成的实物一样具有能量和动量
$\text{D.}$ 德国物理学家普朗克为解释物体热辐射规律, 提出了. 能量子的假说, 他同时最早发现了光电效应,爱因斯坦由于发现了光电效应的规律而获得诺贝尔物理学奖
2023 年 10 月, 南阳一荆门一长沙特高压交流线路工程全线竣工。在输送功率一定时, 分别用 1000 千伏和 500 千伏对同一段线路输电。下列说法正确的是
$\text{A.}$ 高压输电线输送电流之比为 $2: 1$
$\text{B.}$ 高压输电线路电阻损耗功率之比 $1: 4$
$\text{C.}$ 输电线路上电压损失之比为 $1: 4$
$\text{D.}$ 用户得到的功率之比为 $1: 2$
光总是走时间最短的路径。我们在生活中如果也类比光的传播路径行动, 会最快到达目的地。如图甲, 你以恒定的速率从 $A$ 点到 $B$ 过程中需要到河边取一下水, 则类比光的反射路径时间最短。如图乙, 小明在海滩上 $A$ 处发现小张在海中 $B$ 处呼救,已知小明在海滩上奔跑的速度为 $v_1$, 在海水里游泳的速度为 $v_2, v_1>v_2$, 那么小明应该沿图乙中哪条路线去救人用时最短
$\text{A.}$ 沿路线 (1), $\frac{\sin \theta_1}{\sin \theta_2}=\frac{v_1}{v_2}, \theta_1 、 \theta_2$ 分别为路线与海岸线的夹角
$\text{B.}$ 沿路线 (2), 沿 $\mathrm{AB}$ 连线方向直线前进, 总路程最短
$\text{C.}$ 沿路线 (3), $\frac{\cos \alpha}{\cos \beta}=\frac{v_1}{v_2}, \alpha 、 \beta$ 分别为路线与海岸线的夹角
$\text{D.}$ 沿路线 (4), 先到最接近 $B$ 的海边, 再垂直海岸到 $B$, 海水中路程最短
如图, 三个相同金属圆环 $a 、 b 、 c$ 紧套在绝缘圆柱体上, 圆环中通有相同大小的电流,其中 $a 、 b$ 电流方向相反, $a 、 c$ 电流方向相同. 已知环 $a$ 对环 $c$ 的安培力大小为 $F_1$, 环 $b$ 对环 $c$ 的安培力大小为 $F_2$, 则环 $c$ 受到安培力的合力
$\text{A.}$ 大小为 $\left|F_1+F_2\right|$, 方向向左
$\text{B.}$ 大小为 $\left|F_1+F_2\right|$, 方向向右
$\text{C.}$ 大小为 $\left|F_1-F_2\right|$, 方向向左
$\text{D.}$ 大小为 $\left|F_1-F_2\right|$, 方向向右
如图是静电喷涂示意图, 被涂物 $\mathrm{M}$ 带正电, 喷枪喷出的涂料微粒带负电, 在静电力作用下向 $\mathrm{M}$ 运动, 最后吸附在其表面上, 忽略微粒间相互作用, 则涂料微粒在靠近 $\mathrm{M}$ 的过程中
$\text{A.}$ 电势能减少
$\text{B.}$ 电势能增大
$\text{C.}$ 受到的电场力保持不变
$\text{D.}$ 受到的电场力一直减小
如图所示为研究光电效应的实验电路图, 初始时电压表、电流表的示数均为 0 , 用某种单色光照射该光电管时, 电流表的示数不为 0 , 电压表的示数仍为 0 。下列说法正确的是
$\text{A.}$ 向右移动滑动触头 $\mathrm{P}$, 电流表的示数不可能为 0
$\text{B.}$ 向右移动滑动触头 $P$, 电流表的示数可能为 0
$\text{C.}$ 向左移动滑动触头 $\mathrm{P}$, 电流表的示数一定是一直增大
$\text{D.}$ 向左移动滑动触头 $\mathrm{P}$, 电流表的示数可能减小
中国新一代粒子研究利器“超级陶粲”装置关键技术攻关项目已经启动, 静电分析器是其重要的组成部分。静电分析器的两电极之间存在如图所示的静电场, 该静电场中任意一点的电场方向均沿半径方向指向圆心, 大小均满足 $E=\frac{k}{r}$ ( $k$ 为与装置有关的常数, $r$ 为该点到圆心 $O$的距离)。某次实验中一组粒子由人射口 $P$ 进人静电分析器, ${ }_1^3 \mathrm{H}_、{ }_1^2 \mathrm{H}$ 沿轨迹 $\mathrm{I}$ 绕圆心 $O$ 做圆周运动, ${ }_1^1 \mathrm{H}$ 沿轨迹 II 绕圆心 $O$ 做圆周运动。下列说法正确的是
$\text{A.}$ 静电分析器中同一圆周上各点的电场强度相同
$\text{B.}$ 三种粒子的动能都相同
$\text{C.}$ ${ }_1^2 \mathrm{H}$ 粒子在电场中的运动时间最长
$\text{D.}$ ${ }_1^1 \mathrm{H}$ 粒子的向心力最小
如图所示, 单匝线圈 $a b c d$ 在匀强磁场中绕垂直于磁场的 $b c$ 边以角速度 $\omega$ 匀速转动, 线圈内阻不计, 线圈中产生的感应电动势的峰值为 $E_{\mathrm{m}}$, 三个灯泡 $\mathrm{L}_1 、 \mathrm{~L}_2 、 \mathrm{~L}_3$ 的规格完全相同, 变压器可视为理想变压器,在以下各种操作中电路元件都没有损坏。下列说法正确的是
$\text{A.}$ 线圈从图示位置开始计时, 感应电动势的瞬时值表达式为 $e=E_{\mathrm{m}} \cos \omega t$
$\text{B.}$ 仅使滑动触头 $\mathrm{M}$ 上移, 灯泡 $\mathrm{L}_1$ 变暗
$\text{C.}$ 仅使滑动触头 $\mathrm{N}$ 自变阻器 $a$ 端向 $b$ 端移动, 灯泡 $\mathrm{L}_2$ 中的电流一直增大
$\text{D.}$ 仅使滑动触头 $\mathrm{N}$ 自变阻器 $a$ 端向 $b$ 端移动, 灯泡 $\mathrm{L}_3$ 中的电流一直增大
肥皂膜看起来常常是彩色的，雨后公路积水上漂浮的油膜，也经常显现出彩色条
纹。下列现象的原理与之相同的是
$\text{A.}$ 杨氏双缝干涉实验
$\text{B.}$ 影子的形成
$\text{C.}$ 利用光导纤维传递信息，实现光纤通信
$\text{D.}$ 泊松亮斑
如图所示，圆柱形玻璃杯前侧表面上有 a、b、c 三点，粗细均匀的铅笔紧靠玻璃杯后侧外壁竖直放置，且在 b 点正后方。将杯中注满水
$\text{A.}$ 通过 b 点看到铅笔变细
$\text{B.}$ 通过 b 点看到铅笔无变化
$\text{C.}$ 通过 a 点看到铅笔向右侧移
$\text{D.}$ 通过 c 点看到铅笔向右侧
如图 (a)，容器中盛有深度 h = 4cm 的透明液体，一激光束垂直液面射入液体，并在底板发生漫反射，部分漫反射光会在液面发生全反射。恰好发生全反射的光在容器底板上形成直径 $d = 16cm$ 的圆形亮环，如图 (b) 所示。该液体的折射率为
$\text{A.}$ $2$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $\frac{\sqrt{2}}{2}$
制造半导体元件，需要精确测定硅片上涂有的二氧化硅 (SiO2) 薄膜的厚度，把左侧二氧化硅薄膜腐蚀成如图甲所示的劈尖，用波长 λ = 630nm 的激光从上方照射劈尖，观察到在腐蚀区域内有 8 条暗纹，且二氧化硅斜面转为平面的棱 MN 处是亮纹，二氧化硅的折射率为 1.5，则二氧化硅薄膜的厚度为
$\text{A.}$ $1680 \mathrm{~nm}$
$\text{B.}$ $1890 \mathrm{~nm}$
$\text{C.}$ $2520 \mathrm{~nm}$
$\text{D.}$ $3780 \mathrm{~nm}$
如图所示，挡板上安装有宽度可调的一条狭缝，缝后放一个光屏。用单色平行光照射狭缝，狭缝宽度从 0.8mm 调整为 0.4mm，光屏上可能呈现
$\text{A.}$ 图样①变化为图样②
$\text{B.}$ 图样②变化为图样①
$\text{C.}$ 图样③变化为图样④
$\text{D.}$ 图样④变化为图样③
一种光学传感器是通过接收器接收到红绿灯光信号而触发工作的。如图所示，一细束黄色光沿 AB 方向从汽车玻璃外侧 (汽车玻璃可视为两表面平行的玻璃砖) 的 B 点射入，入射角为 i，折射光线刚好沿 BC 方向在汽车玻璃内侧 C 点触发光学传感器。若入射光的颜色发生变化，且入射光的入射位置 B 不变，仍要使折射光线沿 BC 方向在汽车玻璃内侧 C 点触发光学传感器。下列说法正确的是
$\text{A.}$ 若改用绿色光射入，需要入射角 i 减小到某一合适的角
$\text{B.}$ . 若改用红色光射入，需要入射角 i 减小到某一合适的角度
$\text{C.}$ 若改用红色光射入，需要入射角 i 增大到某一合适的角
$\text{D.}$ 改用任何颜色的光射入，都需要入射角 i 减小到某一合适的角度