一、单选题 （共 68 题，每小题 5 分，共 50 分，每题只有一个选项正确）
如图所示, 理想变压器原、副线圈巾数比为 $4: 1$, 灯泡 $a$ 和 $b$ 额定电压相同, 当原线 圈输入 $u=220 \sqrt{2} \sin 10 \pi t(V)$ 的交变电压时, 两灯泡均能正常发光, 且滑动变阻器调节过程 中灯泡不会被烧坏, 下列说法正确的是
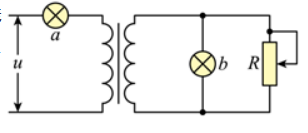
$\text{A.}$ 灯泡的额定电压是 $44 \mathrm{~V}$
$\text{B.}$ 副线圈中交变电流的频率为 $12.5 \mathrm{~Hz}$
$\text{C.}$ 当滑动变阻器的滑片向下滑动时, 灯泡 $a$ 变暗
$\text{D.}$ 当滑动变阻器的滑片向下滑动时, 变压器输入功率变小
摩托车的点火装置原理如图所示。转换器将直流电压转换为 $12 \mathrm{~V}$ 的正弦交流电压, 并 加在高压包 (理想变压器) 的原线圈上, 当副线圈电压的瞬 时值大于 $1.5 \times 10^{+} \mathrm{V}$ 时, 就会使火花塞产生电火花点燃汽 油机工作。以下说法正确的是
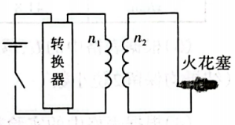
$\text{A.}$ 高压包的副线圈匝数至少是原线圈匝数的 1250 倍
$\text{B.}$ 在电流变化的一个周期内, 火花塞放电一次
$\text{C.}$ 仅升高高压包输人电流的频率, 火花塞放电的频率会增大
$\text{D.}$ 仅升高高压包输人电流的频率, 高压包的输出电压会增大
“羲和号” 是我国首颗太阳探测科学技术试验卫星。如图所示, 该卫星围绕地球的运动视为匀速圆周运 动, 轨道平面与赤道平面接近垂直。卫星每天在相同时刻, 沿相同方向经过地球表面 $A$ 点正上方, 恰好绕 地球运行 $n$ 圈。已知地球半径为地轴 $R$, 自转周期为 $T$, 地球表面重力加速度为 $g$, 则 “羲和号” 卫星轨道 距地面高度为
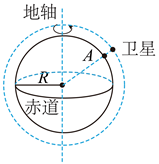
$\text{A.}$ $\left(\frac{g R^2 T^2}{2 n^2 \pi^2}\right)^{\frac{1}{3}}-R$
$\text{B.}$ $\left(\frac{g R^2 T^2}{2 n^2 \pi^2}\right)^{\frac{1}{3}}$
$\text{C.}$ $\left(\frac{g R^2 T^2}{4 n^2 \pi^2}\right)^{\frac{1}{3}}-R$
$\text{D.}$ $\left(\frac{g R^2 T^2}{4 n^2 \pi^2}\right)^{\frac{1}{3}}$
2022 年 12 月 4 日 20 时 09 分, 神舟十四号载人飞船返回舱在东风着降场成功着陆。 三名航天员安全返回。设神舟十四号飞船的质量为 $m$, 飞船与空间站相对静止, 共同在距地面高为 $h$ 处做匀速圆周运动, 地球半径为 $R$, 地球表面重力加速度为 $g$ 。忽略地球自转. 下列关于神舟十四号飞船在轨运行的说法正确的是
$\text{A.}$ 周期为 $\frac{2 \pi}{R} \sqrt{\frac{h^3}{g}}$
$\text{B.}$ 向心加速度为 $\frac{g R^2}{(R+h)^2}$
$\text{C.}$ 角速度为 $R \sqrt{\frac{g}{R+h}}$
$\text{D.}$ 动能为 $\frac{1}{2} m g R$
如图，人造卫星 M、N 在同一平面内绕地心 O 做匀速圆周运动．已知 M、N 连线与 M、
O 连线间的夹角最大为θ，则 M、N 的运动周期之比等
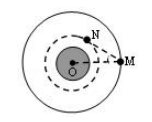
$\text{A.}$ $\sin ^3 \theta$
$\text{B.}$ $\frac{1}{\sin ^3 \theta}$
$\text{C.}$ $\sqrt{\sin ^3 \theta}$
$\text{D.}$ $\sqrt{\frac{1}{\sin ^3 \theta}}$
某次发射卫星时, 先将卫星发射到半径为 $r_1$ 的低轨道上, 运行速度为 $v_1$, 当卫星运动经 过 $A$ 点时, 卫星上的小型火箭发动机点火, 短时间加速, 使卫星进入椭圆轨道运行, 椭圆 轨道的远地点 $B$ 与地心的距离为 $r_2$, 卫星经过 $B$ 点的速度为 $v_B$, 其运行轨迹如图所示。若 规定无穷远处引力势能为 0 , 则引力势能的表达式 $E_p=-\frac{G M m}{r}$, 其中 $G$ 为引力常量, $M$ 为 中心天体质量, $m$ 为卫星的质量, $r$ 为两者质心间距, 若卫星运动过程中仅受万有引力作用, 则下列说法正确的是
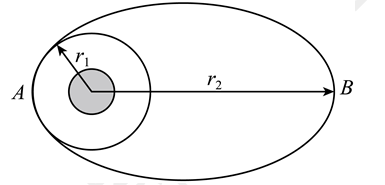
$\text{A.}$ $v_B>v_1$
$\text{B.}$ 卫星在椭圆轨道上 $A$ 点的加速度大于 $B$ 点的加速度
$\text{C.}$ 卫星在 $A$ 点加速后的速度为 $v_A=\sqrt{\frac{1}{2} G M\left(\frac{1}{r_1}-\frac{1}{r_2}\right)+v_B^2}$
$\text{D.}$ 卫星从 $A$ 点运动至 $B$ 点的最短时间为 $t=\frac{1}{v_1} \sqrt{\frac{\left(r_1+r_2\right)^3}{2 r_1}}$
2023 年 1 月 23 日 21 时 31 分, 西安卫星测控中心传来好消息一亚太 $6 \mathrm{E}$ 卫星与独立推进舱星 间分离成功。发射成功 10 天后, 亚太 6E 这颗国产全电推进同步轨道通信卫星正式开启了电推 变轨的旅程。假设电推变轨过程,推进系统沿速度的反方向均匀发射微小的带电粒子, 粒子射 出后瞬间相对卫星的速度大小等于卫星的速度大小的 2 倍, 且粒子在推进系统中的加速时间极 短。可将卫星绕地球的每一圈运动均视为匀速圆周运动。推进系统在相同时间内射出粒子的 质量相同,整个过程卫星的质量变化可忽略。则下列说法正确的是
$\text{A.}$ 卫星受到的推力与轨道半径成正比
$\text{B.}$ 卫星受到的推力与轨道半径无关
$\text{C.}$ 卫星转过一周过程中, 推力做的功与轨道半径的 $\frac{1}{2}$ 次方成正比
$\text{D.}$ 卫星转过一周过程中, 推力做的功与轨道半径无关
材料的力学强度是材料众多性能中被人们极为看重的一种性能，目前已发现的高强度材料碳纳米管的抗拉强度是钢的100倍，密度是钢的 1/6 ，这使得人们有望在赤道上建造垂直于水平面的“太空电梯”。当航天员乘坐“太空电梯”时，地球引力对航天员产生的加速度a与r的关系用图乙中图线A表示，航天员由于地球自转而产生的向心加速度大小与r的关系用图线B表示，其中r为航天员到地心的距离，R为地球半径．关于相对地面静止在不同高度的航天员，下列说法正确的是
$\text{A.}$ 航天员在 r=R 处的线速度等于第一宇宙速度
$\text{B.}$ 图中$r_0$ 为地球同步卫星的轨道半径
$\text{C.}$ 随着r增大，航天员运动的线速度一直减小
$\text{D.}$ 随着r增大，航天员受到电梯舱的弹力减小
2023年春节期间，中国科幻电影《流浪地球2》热映．《流浪地球》系列影片设定：若干年后，太阳上的氢元素将被耗尽，太阳由“氢核聚变”阶段进入“氦核聚变”阶段，并成为一颗红巨星，地球将被太阳吞没、气化．因此，人类启动了“流浪地球”计划．人类的自救之旅的第一阶段是“刹车阶段”，利用2000台安装在地球赤道上的“转向式行星发动机”，通过喷射高能高压的粒子流，推动地球停止自转；第二阶段是“逃逸阶段”，利用“推进式行星发动机”推动地球加速，增大公转速度，逐渐脱离太阳系，开启“流浪”之旅．根据以上素材，结合所学，判断下列说法正确的是
$\text{A.}$ 不考虑其它因素，地球停止自转的过程中，赤道上的物体所受重力逐渐减小
$\text{B.}$ 不考虑其它因素，地球停止自转的过程中，南北极处的物体所受重力逐渐增大
$\text{C.}$ “转向式行星发动机”的喷口方向应该与自转速度方向相反，“推进式行星发动机”的喷口方向应该与公转速度方向相反
$\text{D.}$ 聚变要克服原子核之间的库仑斥力，因此氦核聚变比氢核聚变需要的温度更高
有一种瓜子破壳器如图甲所示，将瓜子放入两圆柱体所夹的凹槽之间，按压瓜子即可破开瓜子壳。破壳器截面如图乙所示，瓜子的剖面可视作顶角为 的扇形，将其竖直放入两完全相同的水平等高圆柱体A、B之间，并用竖直向下的恒力F按压瓜子且保持静止，若此时瓜子壳未破开，忽略瓜子自重，不计摩擦，则
$\text{A.}$ 若仅减小A、B距离，圆柱体A对瓜子的压力变大
$\text{B.}$ 若仅减小A、B距离，圆柱体A对瓜子的压力变小
$\text{C.}$ 若A、B距离不变，顶角 越大，圆柱体A对瓜子的压力越大
$\text{D.}$ 若A、B距离不变，顶角 越大，圆柱体A对瓜子的压力越小
小车在水平地面上沿轨道从左向右运动, 动能一直增加。如果用带箭头的线段表示小车在轨道上相应位 置处所受合力, 下列四幅图可能正确的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
如图所示，载人火箭的顶端的部分装有发射逃生系统，称为逃逸塔，逃逸塔内部包含宇航员乘坐的返回舱。在发射过程中，如果一切正常，逃逸塔不工作，随运载火箭一起升空；如果遇到突发情况，逃逸塔就会自动点火，在短时间脱离运载火箭，从而达到保护宇航员的目的。根据上述信息，下列说法正确的是
$\text{A.}$ 火箭正常发射时，逃逸塔相对运载火箭是运动的
$\text{B.}$ 火箭正常发射时，宇航员相对运载火箭是运动的
$\text{C.}$ 若火箭发射时遇突发情况，逃逸塔将与运载火箭发生相对运动
$\text{D.}$ 若火箭发射时遇突发情况，宇航员与运载火箭始终相对静
如图所示为高空滑索运动，游客利用轻绳通过轻质滑环悬吊沿倾斜滑索下滑。假设某段下滑过程中游客、滑环和轻绳为整体匀速下滑，速度大小为v，整体重力为G ，不计空气阻力，则在这段下滑过程中
$\text{A.}$ 游客的机械能守恒
$\text{B.}$ 轻绳保持竖直
$\text{C.}$ 整体重力势能的减少量等于系统动能的增加量
$\text{D.}$ 重力的功率为Gv
在以速度 $v_0$ 匀速上升的电梯里, 一小球从电梯地板以速度 $v_1\left(v_1>v_0\right)$ 被 坚直向上弹出后又落回到电梯地板, 这一过程中小球没有触碰电梯天花 板, 不计空气阻力, 重力加速度为 $g$ 。则
$\text{A.}$ 小球在空中运动的位移大小一定等于路程
$\text{B.}$ 小球在空中运动的平均速度大于电梯的速度 $v_0$
$\text{C.}$ 小球在空中运动的平均速度小于电梯的速度 $v_0$
$\text{D.}$ 小球从抛出到离电梯天花板最近时, 电梯的位移为 $\frac{\left(v_1-v_0\right) v_0}{g}$
圆柱形弹簧的劲度系数 $k$ 与弹簧处于原长时的长度 $L$ 、横截面积 $S$ 有关, 理论与实践都表明 $k=Y \frac{S}{L}$, 其中 $Y$ 是一个由材料决定的常数, 材料学上称之为杨氏模量. 在国际单位制中, 杨氏模量 $Y$ 的单位可表示为
$\text{A.}$ $\mathrm{N} / \mathrm{m}^2$
$\text{B.}$ $\mathrm{N} \cdot \mathrm{m}^2$
$\text{C.}$ $\mathrm{N}$
$\text{D.}$ $\mathrm{N} / \mathrm{m}$
如图所示, 压缩机通过光滑活塞在汽缸内往复运动来压缩气体, 活塞的中心 $A$ 与转轮在同一平面内, $O$ 为转轮圆心, $B$ 为转轮边缘上一点, $A 、 B$ 处通过较链连接在轻杆两端, 转轮绕 $O$ 点做角速度为 $\omega$ 的匀速圆周运动. 已知转轮半径为 $r$, 则当 $B$ 点从 $O$ 点水平右侧转动到 $O$ 点水平左侧的过程中
$\text{A.}$ 轻杆对活塞做负功
$\text{B.}$ 活塞速度保持不变
$\text{C.}$ 当 $O B$ 垂直于 $A B$ 时,活塞速度为 $\omega r$
$\text{D.}$ 当 $O B$ 垂直于 $A O$ 时, 活塞速度为 $\omega r$
某实验小组用数字传感器探究橡皮筋的弹性规律, 实验过程中先缓慢拉长橡皮筋, 然后逐渐恢复至原长, 记录实验数据后, 以橡皮筋的形变量 $\Delta x$ 为横坐标, 橡皮筋的弹力 $F$ 为纵坐标建立直角坐标系, 如图所示, 对应 $O \rightarrow A \rightarrow B \rightarrow C \rightarrow O$ 的过程. 下列判断正确的是
$\text{A.}$ 由图像可知, 橡皮筋的弹性规律满足胡克定律
$\text{B.}$ 产生相等弹力时, 橡皮筋的形变量相等
$\text{C.}$ $A \rightarrow B$ 过程中,橡皮筋的劲度系数增大
$\text{D.}$ 在整个过程中,外力对橡皮筋做正功
图甲为土星探测器拍摄的照片 (图乙为其示意图), 土卫三十五号位于土星内环和外环之间的缝隙里, 由于其对所经过区域的引力作用, 原本平滑的土星环边沿泛起 “涟渏”. 已知两土星环由大量碎块组成且绕土星运行方向相同, 土卫三十五号轨道与两土星环始终位于同一平面,根据图乙中的信息,下列说法正确的是
$\text{A.}$ 内环绕行角速度有可能小于外环
$\text{B.}$ 内环绕行周期有可能大于外环
$\text{C.}$ 土卫三十五号运行方向与两环绕行方向相同且顺时针运行
$\text{D.}$ 土卫三十五号运行方向与两环绕行方向相反且逆时针运行
天问一号于 2021 年 2 月 10 日与火星交会，进入环绕火星轨道。如图所示为其简化飞行路线图，在 P 点进入地火转移轨道，在 Q 点被火星俘获。已知火星的轨道半径是地球轨道半径的 1.5 倍，则下列说法正确的是
$\text{A.}$ 天问一号在地火转移轨道的周期大于火星的公转周期
$\text{B.}$ 相等时间内天问一号与太阳的连线扫过的面积等于火星与太阳的连线扫过的面积
$\text{C.}$ 在地火转移轨道上天问一号经过 P 点的速度小于经过 Q 点的速度
$\text{D.}$ 天问一号从发射到被火星俘获，经历的时间约 255 天
2023 年 5 月 30 日 9 时 31 分, 我国自主研发的长征二号 $F$ 遥十六运载火箭, 搭载景海鹏、朱杨柱、桂海潮三名航天员的神舟十六号载人飞船, 在酒泉卫星发射中心成功发射。神舟十六号飞船入轨后在停泊轨道 (I) 上进行数据确认, 后择机经转移轨道 (II) 于当日 16 时 29 分与中国空间站组合体完成自主快速交会对接, 其变轨过程可简化如右图所示, 已知停泊轨道半径近似为地球半径 $R$, 中国空间站轨道距地面的平均高度为 $h$, 飞船在停泊轨道上的周期为 $T_1$, 则
$\text{A.}$ 飞船在停泊轨道上的速度大于第一宇宙速度
$\text{B.}$ 飞船在转移轨道上 $P 、 Q$ 两点的速率之比为 $R:(R+h)$
$\text{C.}$ 若飞船在 I 轨道的点 $P$ 点火加速, 至少经过时间 $\frac{T_1}{2} \sqrt{\left(1+\frac{h}{2 R}\right)^3}$, 才能在 II 轨道的 $Q$ 点与空间站完成交会对接
$\text{D.}$ 中国空间站的物品或宇航员可以漂浮, 说明此时它们或他们不受地球引力作用
位于地球赤道上的一物体 $A$, 质量为 $m$, 已知当地的重力加速度为 $g$, 地球半径为 $R$, 引力常量为 $G$,忽略地球自转的影响, 则下列说法正确的是
$\text{A.}$ 根据以上条件,能计算出地球质量 $M$
$\text{B.}$ 由以上条件, 可求得地球的平均密度为 $\rho=\frac{g}{4 G \pi}$
$\text{C.}$ 与地球同步卫星相比, $A$ 的角速度更大
$\text{D.}$ $A$ 的线速度大于第一宇宙速度
将一质量为 $m$ 的物体分别放到地球的南北两极点时, 该物体的重力均为 $\mathrm{mg}_0$ 。将该物体放在地球赤道上时, 该物体的重力为 $\mathrm{mg}$; 假设地球可视为质量均匀分布的球体, 半径为 $R$, 已知引力常量为 $G$, 则由以上信息可得出
$\text{A.}$ $g_0 < g$
$\text{B.}$ 地球的质量为 $\frac{g R^2}{G}$
$\text{C.}$ 地球自转的角速度为 $\omega=\sqrt{\frac{g_0-g}{R}}$
$\text{D.}$ 地球的平均密度为 $\rho=\frac{3 g_0}{4 G R}$
哈勃望远镜被称为宇宙之眼, 人类利用哈勃望远镜观察发现了很多新天体, 现观察发现银河系中存在一颗行星, 在若干年前并未发生自转, 若干年后的今天正在自转且越转越快, 经测量, 该星球现在以角速度 $\omega$ 自转, 同一物体对赤道处的压力减为原来的 $\frac{3}{4}$, 该星球可视为球体, 则该星球的平均密度为
$\text{A.}$ $\frac{3 \omega^2}{2 \pi G}$
$\text{B.}$ $\frac{9 \omega^2}{4 \pi G}$
$\text{C.}$ $\frac{\omega^2}{\pi G}$
$\text{D.}$ $\frac{3 \omega^2}{\pi G}$
宇航员驾驶宇宙飞船绕质量分布均匀的一星球做匀速圆周运动, 测得飞船线速度大小的二次方与轨道半径的倒数的关系图如图中实线所示, 该图线 (直线) 的斜率为 $k$, 图中 $r_0$ (该星球的半径) 为已知量。引力常量为 $G$, 下列说法正确的是
$\text{A.}$ 该星球的密度为 $\frac{3 G}{4 \pi k r_0^3}$
$\text{B.}$ 该星球的自转周期为 $\sqrt{\frac{r_0^2}{k}}$
$\text{C.}$ 该星球表面的重力加速度大小为 $\frac{k}{r_0^2}$
$\text{D.}$ 该星球的第一宇宙速度为 $\sqrt{\frac{k}{r_0}}$
在 2023 年 “中国航天日” 主场活动启动仪式上, 国家航天局和中国科学院联合发布了中国首次火星探测火星全球影像图。若在火星上将一小球以大小为 $v_0$ 的速度坚直向上抛出, 经时间 $t$ 小球落回原处, 已知火星的半径为 $R$, 引力常量为 $G$, 不考虑火星的自转, 不计空气阻力, 则下列说法正确的是
$\text{A.}$ 火星的质量为 $\frac{2 v_0 R^2}{G t}$
$\text{B.}$ 火星的平均密度为 $\frac{3 v_0}{4 \pi G R t}$
$\text{C.}$ 火星的第一宇宙速度为 $\sqrt{\frac{v_0 R}{t}}$
$\text{D.}$ 环绕火星表面运行的卫星的周期为 $\pi \sqrt{\frac{2 R t}{v_0}}$
由于地球自转的影响, 地球表面的重力加速度会随纬度的变化而有所不同。已知地球表面两极处的重力加速度大小为 $g_0$, 在赤道处的重力加速度大小为 $g$, 地球自转的周期为 $T$, 引力常量为 $G$ 。假设地球可视为质量均匀分布的球体。下列说法不正确的是
$\text{A.}$ 质量为 $m$ 的物体在地球北极受到的重力大小为 $\mathrm{mg}_0$
$\text{B.}$ 质量为 $m$ 的物体在地球赤道上受到的万有引力大小为 $\mathrm{mg}$
$\text{C.}$ 地球的半径为 $\frac{\left(g_0-g\right) T^2}{4 \pi^2}$
$\text{D.}$ 地球的密度为 $\frac{3 g_0 \pi}{G T^2\left(g_0-g\right)}$
如图是某农家院内打出一口深度为 d 的水井，如果质量分布均匀的球壳对壳内物体的引力为零，地球可以看作是质量分布均匀的球体，地球半径为 R，则水井底部和离地面高度为 d 处的重力加速度大小之比为
$\text{A.}$ $\frac{R-d}{R}$
$\text{B.}$ $\frac{\left(R^2-d^2\right)(R+d)}{R^3}$
$\text{C.}$ $\frac{R^2-d^2}{R}$
$\text{D.}$ $\frac{\left(R^2-d^2\right)(R+d)}{R^2}$
一半径为 $R$ 、质量分布均匀的球形行星绕其自转轴匀速转动。若质量为 $m$ 的物体在该行星两极时的重力为 $G_0$, 在该行星赤道上的重力为 $\frac{3 G_0}{4}$, 设行星自转的角速度为 $\omega$, 环绕该行星表面做匀速圆周运动的卫星的速率为 $v$, 则下列表达式正确的是
$\text{A.}$ $v=\sqrt{\frac{G_0 R}{4 m}}$
$\text{B.}$ $v=\sqrt{\frac{G_0 R}{m}}$
$\text{C.}$ $\omega=\sqrt{\frac{G_0}{2 m R}}$
$\text{D.}$ $\omega=\sqrt{\frac{G_0}{m R}}$
如图, 水平弹簧右端固定在坚直墙壁上, 左端连接在物块上, 水平面光滑. 开始时物块静止, 弹簧处于原长. 一颗子弹以水平速度 $v_0$ 射人物块, 并留在物块中. 若子弹和物块作用时间极短,下列有关说法中正确的是
$\text{A.}$ 从子弹开始打物块到弹簧压缩至最短, 子弹、物块、弹簧组成的系统动量守恒
$\text{B.}$ 从子弹开始打物块到弹簧压缩至最短, 子弹、物块、弹簧组成的系统机械能守恒
$\text{C.}$ 从子弹开始打物块到与物块共速, 子弹、物块组成的系统动量守恒
$\text{D.}$ 子弹和物块一起压缩弹簧的过程中, 物块、子弹、弹簧组成的系统动量守恒
二十四节气是中华民族的文化遗产. 地球沿椭圆形轨道绕太阳运动, 所处四个位置分别对应北半球的四个节气, 如图所示. 下列关于地球绕太阳公转的说法中, 正确的是
$\text{A.}$ 冬至时线速度最大
$\text{B.}$ 夏至和冬至时的角速度相同
$\text{C.}$ 夏至时向心加速度最大
$\text{D.}$ 可根据地球的公转周期求出地球的质量
图甲为挂在架子上的双层晾衣篮. 上、下篮子完全相同且保持水平, 每个篮子由两个质地均匀的圆形钢圈穿进网布构成, 两篮通过四根等长的轻绳与钢圈的四等分点相连, 上篮钢圈用另外四根等长轻绳系在挂钧上. 晾衣篮的有关尺寸如图乙所示, 则图甲中上、下各一根绳中的张力大小之比为
$\text{A.}$ $1: 1$
$\text{B.}$ $2: 1$
$\text{C.}$ $5: 2$
$\text{D.}$ $5: 4$
下列选项中, 所画弹力方向不正确的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
如图所示, 司机为方便卸货, 在车厢尾部与地面之间搭建了一个斜面。其中车厢尾部到地面的高度为 $1.2 \mathrm{~m}$,车厢尾部到地面间的木板长度为 $2 \mathrm{~m}$ 。若货物恰好能沿木板匀速下滑, 则货物与木板间的动摩擦因数为
$\text{A.}$ 0.75
$\text{B.}$ 0.8
$\text{C.}$ 0.6
$\text{D.}$ 0.5
教室里要挂一个城市文化宣传框。若粘钩的承重能力足够大, 则以下哪种悬挂方式, 绳子的拉力最小
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
如图所示, 横载面为四分之一圆、质量为 $M$ 的柱体 $\mathrm{B}$ 放在粗糙水平地面上, 一竖直固定的挡板与柱体最左侧相切, 质量为 $m$ 的小球 $a$ 恰能静止在挡板和柱体之间。现拿走小球 $a$, 将质量也为 $m$ 、但体积比 $a$ 大的小球 $b$贴着挡板轻放到柱体 B 上。小球与挡板、小球与柱体之间无摩擦力。下列说法正确的是
$\text{A.}$ 小球 $b$ 对挡板的压力大于小球 $a$ 对挡板的压力
$\text{B.}$ 小球 $b$ 对柱体的压力大于小球 $a$ 对柱体的压力
$\text{C.}$ 地面对柱体的支持力不变
$\text{D.}$ 柱体受到地面的摩擦力不变
高空中, 一架飞机沿水平方向做匀加速直线运动, 加速度大小为 $1 \mathrm{~m} / \mathrm{s}^2$, 每隔 $1 \mathrm{~s}$ 从飞机上落下一物体, 不计空气阻力, 重力加速度取 $10 \mathrm{~m} / \mathrm{s}^2$, 这些物体在空中排列的图线是一条
$\text{A.}$ 倾斜直线, 直线的斜率为 10
$\text{B.}$ 倾斜直线, 直线的斜率为 $\frac{1}{10}$
$\text{C.}$ 坚直直线
$\text{D.}$ 抛物线, 其竖直分运动是自由落体
如图所示, 坚直墙壁上固定一支架 $M O N$, 其中水平杆 $O M$ 表面粗䊁, 倾斜杆 $O N$ 表面光滑。杆 $O M 、$ 、杆 $O N$ 上分别套有小环 $P 、 Q$, 两环由不可伸长的轻质细绳相连,处于平衡状态, 现将 $P$ 环向右移动少许重新达到平衡。那么移动后的平衡状态和原来的平衡状态 (图示状态) 相比较, 下列说法正确的是
$\text{A.}$ 杆 $O N$ 对环 $Q$ 的弹力一定变大
$\text{B.}$ 细绳的拉力可能变大
$\text{C.}$ 环 $P$ 与杆 $O M$ 间的弹力一定变大
$\text{D.}$ 环 $P$ 的摩擦力可能不变
如图甲, “星下点” 是指卫星和地心莲线与地球表面的交点。图乙是航天控制中心大屏幕上显示卫星 FZO1 的“星下点”在一段时间内的轨迹,已知地球同步卫星的轨道半径为 $r=6.6 R(R$是地球的半径), FZO1 绕行方向与地球自转方向一致,则下列说法正确的是
$\text{A.}$ 卫星 FZ01 的轨道半径约为 $\frac{r}{3}$
$\text{B.}$ 卫星 FZ01 的轨道半径约为 $\frac{r}{5}$
$\text{C.}$ 卫星 FZ01 可以记录到南极点的气候变化
$\text{D.}$ 卫星 FZ01 不可以记录到北极点的气候变化
无线充电宝可通过磁吸力吸附在手机背面, 如图甲所示为科创小组某同学手握手机 (手不接触充电宝), 利用手机软件记录坚直放置的手机及吸附的充电宝从静止开始在坚直方向上的一次变速运动过程 (手机与充电宝始终相对静止), 记录的加速度 $a$ 随时间 $t$ 变化的图像如图乙所示 (规定向上为正方向), $t_2$ 时刻充电宝速度为零, 且最终处于静止状态。已知手机的质量为 $0.3 \mathrm{~kg}$, 无线充电宝质量为 $0.2 \mathrm{~kg}$, 手机与充电宝之间的动摩擦因数 $\mu=0.5$, 最大静摩擦力等于滑动摩擦力, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$ 。在该过程中下列说法正确的是
$\text{A.}$ 充电宝在 $t_1$ 与 $t_2$ 时刻所受的摩擦力方向相反
$\text{B.}$ $t_3$ 时刻充电宝受的摩擦力大小为 $3.6 \mathrm{~N}$
$\text{C.}$ 充电宝受到的静摩擦力的最大值为 $7.5 \mathrm{~N}$
$\text{D.}$ 充电宝与手机之间的吸引力大小至少为 $10 \mathrm{~N}$
如图所示, 固定光滑斜面倾角 $\theta=60^{\circ}$, 其底端与竖直面内半径为 $R$ 的固定光滑圆弧轨道相切, 位置 $D$ 为圆弧轨道的最低点。质量为 $2 m$ 的小球 $A$ 和质量为 $m$ 的小环 $B$ (均可视为质点) 用 $L=1.5 R$ 的轻杆通过轻质较链相连。 $B$ 套在光滑的固定竖直长杆上, 杆和圆轨道在同一坚直平面内, 杆过轨道圆心 $O$, 初始轻杆与斜面垂直。在斜面上由静止释放 $A$, 假设在运动过程中两杆不会碰撞, 小球能滑过 $D$ 点且通过轨道连接处时无能量损失 (速度大小不变), 重力加速度为 $g$, 从小球 $A$ 由静止释放到运动至最低点的过程中, 下列判断正确的是
$\text{A.}$ $A$ 和 $B$ 组成的系统的机械能不守恒
$\text{B.}$ 刚释放时小球 $A$ 的加速度大小为 $\frac{\sqrt{3}}{2} g$
$\text{C.}$ 小环 $B$ 速度最大时轻杆弹力为 $m g$
$\text{D.}$ 小球 $A$ 运动到最低点时的速度大小为 $\frac{\sqrt{3 g R}}{3}$