单选题 (共 6 题 ),每题只有一个选项正确
某医疗公司引进新技术设备后, 销售收入(包含医疗产品收入和其他收入) 逐年翻一番,据 统计该公司销售收入情况如图 1 所示, 则下列说 法错误的是
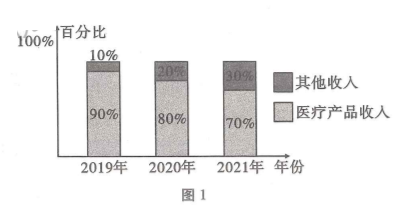
$\text{A.}$ 该地区 2021 年的销售收入是 2019 年的 4 倍
$\text{B.}$ 该地区 2021 年的医疗产品收入比 2019 年和 2020 年的医疗产品收入总和还要多
$\text{C.}$ 该地区 2021 年其他收入是 2020 年的其他收入的 3 倍
$\text{D.}$ 该地区 2021 年的其他收入是 2019 年的其他收入的 6 倍
小明家订了一份牛奶, 送奶人可能在早上 $6:30 \sim 7:00$ 间把牛奶送到小明家, 小明出门去 上学的时间在早上 $6:50 \sim 7:10$ 之间, 则小明有离丙家之前能得到牛奶的概率是
$\text{A.}$ $\frac{1}{12}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{7}{8}$
$\text{D.}$ $\frac{11}{12}$
如图 3, 已知四面体 $A B C D$ 中, $A B=A C=B D=C D=2 \sqrt{2}, A D=B C=2$, $E, F$ 分别是 $A D, B C$ 的中点. 若用一个与直线 $E F$ 垂直, 且与四面体 的每一个面都相交的平面 $\alpha$ 去截该四面体, 由此得到一个多边形截 面, 则该多边形截面面积的最大值为
$\text{A.}$ $1$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $2$
$\text{D.}$ $2 \sqrt{2}$
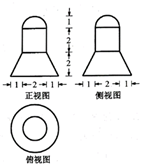
某几何体的三视图如图所示 (单位: $\mathrm{cm}$ ), 则该几何体的体积 (单位: $\mathrm{cm}^3$ ) 是
$\text{A.}$ $22 \pi$
$\text{B.}$ $8 \pi$
$\text{C.}$ $\frac{22}{3} \pi$
$\text{D.}$ $\frac{16}{3} \pi$
. 已知 $2^a=5, \log _8 3=b$, 则 $4^{a-3 b}=$
$\text{A.}$ $25$
$\text{B.}$ $5$
$\text{C.}$ $\frac{25}{9}$
$\text{D.}$ $\frac{5}{3}$
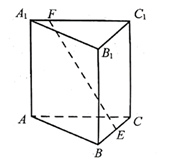
如图, 已知正三棱柱 $A B C-A_1 B_1 C_1, A C=A A_1, E, F$ 分别是棱 $B C, A_1 C_1$ 上的点. 记 $E F$ 与 $A A_1$ 所成的角为 $\alpha, E F$ 与平面 $A B C$ 所成的角为 $\beta$, 二面角 $F-B C-A$ 的平面 角为 $\gamma$, 则
$\text{A.}$ $\alpha \leq \beta \leq \gamma$
$\text{B.}$ $\beta \leq \alpha \leq \gamma$
$\text{C.}$ $\beta \leq \gamma \leq \alpha$
$\text{D.}$ $\alpha \leq \gamma \leq \beta$