单选题 (共 6 题 ),每题只有一个选项正确
我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的 6 个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有 3 个阳爻的概率是 ( )
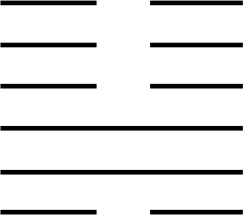
$\text{A.}$ $5 \over 16$
$\text{B.}$ $11 \over 32$
$\text{C.}$ $21 \over 32$
$\text{D.}$ $11 \over 16$
执行如图所示的程序框图,输出的 s 值为 ( )
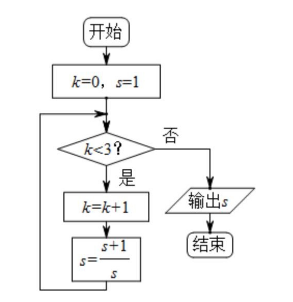
$\text{A.}$ 2
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{5}{3}$
$\text{D.}$ $\frac{8}{5}$
已知 $a=\sin \frac{\pi}{4}, b=e^{\ln \frac{1}{2}}, c=\frac{\pi}{6}$ 执行如图所示的程序框图, 输出的值为

$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\frac{\pi}{6}$
$\text{D.}$ $1$
执行如图所示的程序框图, 输出的结果为 258 , 则判断框内可填入的条 件为
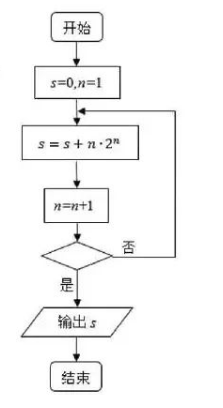
$\text{A.}$ $n \geq 4$ ?
$\text{B.}$ $n \geq 5$ ?
$\text{C.}$ $n \geq 6$ ?
$\text{D.}$ $n \geq 7$ ?
执行如下图所示的程序框图, 则输出的 $T$ 为
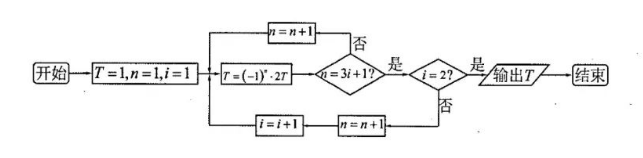
$\text{A.}$ $128$
$\text{B.}$ $-32$
$\text{C.}$ $16$
$\text{D.}$ $-64$
如图所示的函数图象与 $x$ 轴均有交点, 其中不能用二分法求图中交点横坐标的是
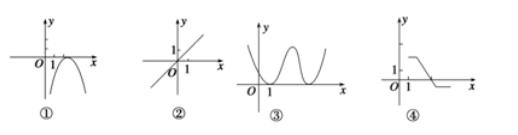
$\text{A.}$ (1)(3)
$\text{B.}$ (2)(4)
$\text{C.}$ (1)(2)
$\text{D.}$ (3)(4)