单选题 (共 6 题 ),每题只有一个选项正确
已知三棱雉 $S-A B C$ 的底面 $A B C$ 是等边三角形, 平面 $S A C \perp$ 平面 $A B C, S A=S C, \angle A S C=$ $90^{\circ}, M$ 为 $S B$ 上一点, 且 $A M \perp B C$. 设三棱雉 $S-A B C$ 外接球球心为 $O$, 则
$\text{A.}$ 直线 $O M \perp$ 平面 $S A C, O A \perp S B$
$\text{B.}$ 直线 $O M / /$ 平面 $S A C, O A \perp S B$
$\text{C.}$ 直线 $O M \perp$ 平面 $S A C$, 平面 $O A M \perp$ 平面 $S B C$
$\text{D.}$ 直线 $O M / /$ 平面 $S A C$, 平面 $O A M \perp$ 平面 $S B C$
圆台的上、下底面半径分别是 $r=1, R=4$, 圆台的高为 4 , 则该圆台的侧面积
$\text{A.}$ $16 \pi$
$\text{B.}$ $20 \pi$
$\text{C.}$ $25 \pi$
$\text{D.}$ $30 \pi$
已知正四棱雉 (底面为正方形, 且顶点在底面的射影为正方形的中心的棱雉为正四棱雉) $P-A B C D$ 的底面正方形边长为 2 , 其内切球 $O$ 的表面积为 $\frac{\pi}{3}$, 动点 $Q$ 在正方形 $A B C D$ 内运 动, 且满足 $O Q=O P$, 则动点 $Q$ 形成轨迹的周长为
$\text{A.}$ $\frac{2 \pi}{11}$
$\text{B.}$ $\frac{3 \pi}{11}$
$\text{C.}$ $\frac{4 \pi}{11}$
$\text{D.}$ $\frac{5 \pi}{11}$
刍(chú)甍(méng)是中国古代算数中的一种几何体,其结构特征是:底面为长方形,上棱和底面平行,且长度不等于底面平行的棱长的五面体,是一个对称的楔形体
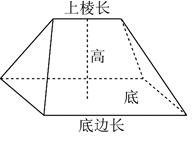
已知一个刍甍底边长为6,底边宽为4,上棱长为2,高为2,则它的表面积是
$\text{A.}$ $24 \sqrt{2}$
$\text{B.}$ $24+24 \sqrt{2}$
$\text{C.}$ $24+24 \sqrt{5}$
$\text{D.}$ $24+16 \sqrt{2}+8 \sqrt{5}$
以一个给定的正 2022 边形的 4 个顶点为顶点的梯形称为好梯形,则好梯形的个数为
$\text{A.}$ $1009 \cdot 1010 \cdot 1011$
$\text{B.}$ $1008 \cdot 1009.1010$
$\text{C.}$ $1000 \cdot 1011 \cdot 1012$
$\text{D.}$ 其它三个选项均不对
四面体 $A B C D$ 中, $A B=C D=3$, 其余棱长均为 $4, E, F$ 分别为 $A B, C D$ 上的点 (不含端点), 则
$\text{A.}$ 不存在 $E$, 使得 $E F \perp C D$
$\text{B.}$ 存在 $E$, 使得 $D E \perp C D$
$\text{C.}$ 存在 $E$, 使得 $D E \perp$ 平面 $A B C$
$\text{D.}$ 存在 $E, F$, 使得平面 $C D E \perp$ 平面 $A B F$