单选题 (共 6 题 ),每题只有一个选项正确
$f(x)=2 f(4-x)-x^{2}+2 x-1$, 则 $y=f(x)$ 在 $(2, f(2))$ 处的切线方程为 ( )
$\text{A.}$ $2 x-y-3=0$
$\text{B.}$ $2 x+3 y+7=0$
$\text{C.}$ $2 x-y+3=0$
$\text{D.}$ $2 x+3 y-7=0$
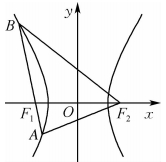
如图, 已知 $F_{1}, F_{2}$ 分别为双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左右焦点, 过 $F_{1}$ 的直线与双 曲线 $C$ 的左支交于 $A 、 B$ 两点, 连接 $A F_{2}, B F_{2}$, 在 $\triangle A B F_{2}$ 中, $A B=B F_{2}, \cos \angle A B F_{2}=\frac{31}{32}$, 则双曲线的离心率为 ( )
$\text{A.}$ $2$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\frac{3 \sqrt{2}}{2}$
若直线 $\frac{x}{a}+\frac{y}{b}=1$ 与圆 $x^{2}+y^{2}=1$ 有公共点, 则( )
$\text{A.}$ $a^{2}+b^{2} \leqslant 1$
$\text{B.}$ $a^{2}+b^{2} \geqslant 1$
$\text{C.}$ $\frac{1}{a^{2}}+\frac{1}{b^{2}} \leqslant 1$
$\text{D.}$ $\frac{1}{a^{2}}+\frac{1}{b^{2}} \geqslant 1$
已知双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的渐近线与抛物线 $y=x^{2}+1$ 相 切, 则该双曲线的离心率为 ( )
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2$
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ $\sqrt{6}$
已知直线 $y=x+1$ 与曲线 $y=\ln (x+a)$ 相切, 则 $a$ 的值为 ( )
$\text{A.}$ $1$
$\text{B.}$ $2$
$\text{C.}$ $-1$
$\text{D.}$ $-2$
已知椭圆 $\mathrm{C}: \frac{\mathrm{x}^{2}}{2}+\mathrm{y}^{2}=1$ 的右焦点为 $\mathrm{F}$, 右准线为 $\mathrm{I}$, 点 $\mathrm{A} \in \mathrm{I}$, 线段 $\mathrm{AF}$ 交 $C$ 于点 $B$, 若 $\overrightarrow{F A}=3 \overrightarrow{F B}$, 则 $|\overrightarrow{A F}|=(\quad)$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 3