单选题 (共 6 题 ),每题只有一个选项正确
已知函数$f(x)=\sin(\omega x+\varphi)$在区间$\left(\dfrac{\pi}{6},\dfrac{2\pi}{3}\right)$单调递增,直线$x=\dfrac{\pi}{6}$和$x=\dfrac{2\pi}{3}$为函数$y=f(x)$的图象的两条对称轴,则$f\left(-\dfrac{5\pi}{12}\right)=$( )
$\text{A.}$ $-\dfrac{\sqrt{3}}{2}$
$\text{B.}$ $-\dfrac{1}{2}$
$\text{C.}$ $\dfrac{1}{2}$
$\text{D.}$ $\dfrac{\sqrt{3}}{2}$
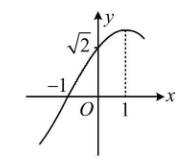
函数$f(x)=A\cos(\omega x+\varphi)\left(A>0,\omega>0,|\varphi| < \dfrac{\pi}{2}\right)$的部分图象如图所示,则$f\left(\dfrac{7}{3}\right)=$( )
$\text{A.}$ $\dfrac{1}{2}$
$\text{B.}$ $\dfrac{\sqrt{2}}{2}$
$\text{C.}$ $\dfrac{\sqrt{3}}{3}$
$\text{D.}$ $1$
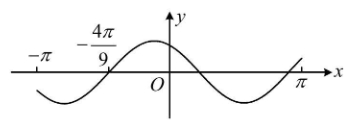
设$f(x)=\cos\left(\omega x+\dfrac{\pi}{6}\right)$在$[-\pi,\pi]$的图象大致如下图,则$f(x)$的最小正周期为( )
$\text{A.}$ $\dfrac{10\pi}{9}$
$\text{B.}$ $\dfrac{7\pi}{6}$
$\text{C.}$ $\dfrac{4\pi}{3}$
$\text{D.}$ $\dfrac{3\pi}{2}$
为了得到函数$y=2\sin\left(x+\dfrac{\pi}{3}\right)$的图象,只需把函数$y=2\sin x$的图象( )
$\text{A.}$ 向左平移$\dfrac{\pi}{6}$个单位长度
$\text{B.}$ 向右平移$\dfrac{\pi}{6}$个单位长度
$\text{C.}$ 向左平移$\dfrac{\pi}{3}$个单位长度
$\text{D.}$ 向右平移$\dfrac{\pi}{3}$个单位长度
要得到函数$y=\cos\left(2x-\dfrac{\pi}{4}\right)$的图象,只需要将函数$y=\cos2x$的图象( )
$\text{A.}$ 向左平移$\dfrac{\pi}{8}$个单位
$\text{B.}$ 向右平移$\dfrac{\pi}{8}$个单位
$\text{C.}$ 向左平移$\dfrac{\pi}{4}$个单位
$\text{D.}$ 向右平移$\dfrac{\pi}{4}$个单位
已知函数$f(x)=\sin(\omega x+\varphi)\left(\omega>0,0 < \varphi < \dfrac{\pi}{2}\right)$的最小正周期为$\pi$,且满足$f(x+\varphi)=f(\varphi-x)$,则要得到函数$f(x)$的图象,可将$g(x)=\cos\omega x$的图象( ).
$\text{A.}$ 向左平移$\dfrac{\pi}{3}$个单位长度
$\text{B.}$ 向右平移$\dfrac{\pi}{3}$个单位长度
$\text{C.}$ 向左平移$\dfrac{\pi}{6}$个单位长度
$\text{D.}$ 向右平移$\dfrac{\pi}{6}$个单位长度