单选题 （共 6 题 ），每题只有一个选项正确
函数$f(x)=\dfrac{2^x-2^{-x}}{2^{|x|}}$的部分图象大致为（ ）.
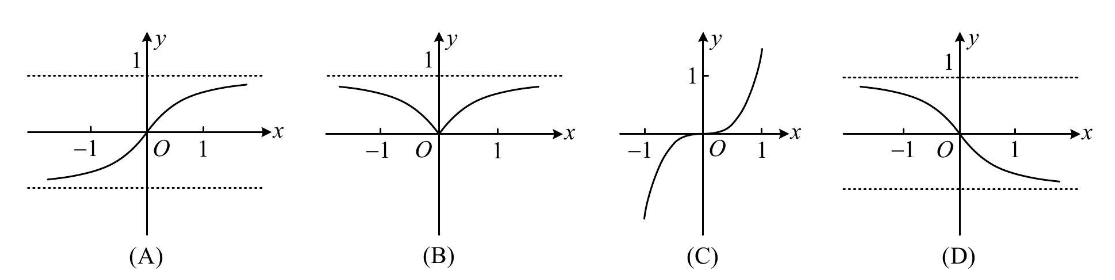
$\text{A.}$
$\text{B.}$
已知函数$f(x)=e^{|x|}-2x^2$,则$f(x)$的图象可能是（ ）.
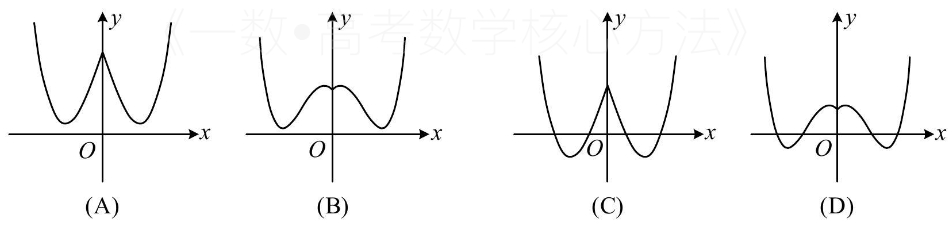
$\text{A.}$
$\text{B.}$
已知 $a=\frac{\ln 2}{2}, b=\frac{\ln 6}{6}, c=\frac{\ln 7}{7}$, 则
$\text{A.}$ $ c>b>a $
$\text{B.}$ $b>a>c$
$\text{C.}$ $b>c>a$
$\text{D.}$ $a>b>c$
函数 $ f(x)=\dfrac{x \log _2|x|}{2^x+2^{-x}} $ 的部分图象大致是
$\text{A.}$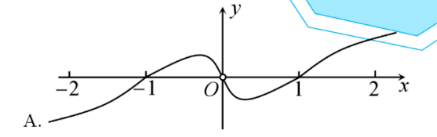 
$\text{B.}$ 
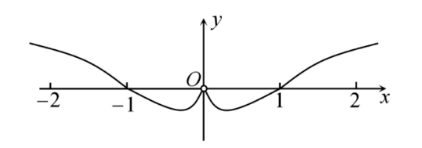$\text{C.}$ 
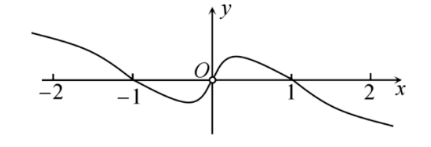$\text{D.}$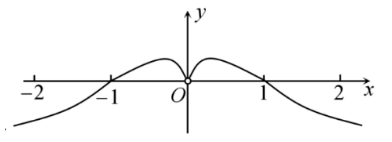 
设函数 $f(x)=2^{x(x-a)}$ 在区间 $(0,1)$ 上单调递减, 则 $a$ 的取值范围是
$\text{A.}$ $(-\infty,-2]$
$\text{B.}$ $[-2,0)$
$\text{C.}$ $(0,2]$
$\text{D.}$ $[2,+\infty)$
指数函数 $y=a^x$ 的图象如图所示, 则 $y=a x^2+x$ 图象顶点横坐标的取值范围是
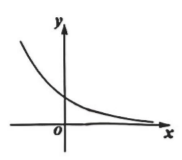
$\text{A.}$ $\left(-\infty,-\frac{1}{2}\right)$
$\text{B.}$ $\left(-\frac{1}{2}, 0\right)$
$\text{C.}$ $\left(0, \frac{1}{2}\right)$
$\text{D.}$ $\left(-\frac{1}{2},+\infty\right)$