单选题 (共 6 题 ),每题只有一个选项正确
设 $R$ 为幂级数 $\sum_{n=1}^{\infty} a_n r^n$ 的收敛半径, $r$ 是实数, 则 ( )
$\text{A.}$ $\sum_{n=1}^{\infty} a_n r^n$ 发散时, $|r| \geq R$
$\text{B.}$ $\sum_{n=1}^{\infty} a_n r^n$ 发散时, $|r| \leq R$
$\text{C.}$ $|r| \geq R$ 时, $\sum_{n=1}^{\infty} a_n r^n$ 发散
$\text{D.}$ $|r| \leq R$ 时, $\sum_{n=1}^{\infty} a_n r^n$ 发散
设数列 $\left\{\mathrm{x}_{\mathrm{n}}\right\}$ 与 $\{\mathrm{y_n}\}$ 满足 $\lim _{\mathrm{n} \rightarrow \infty} x_n y_n=0$, 则下列命题正确的是
$\text{A.}$ 若 $\left\{x_n\right\}$ 发散, 则 $\left\{y_n\right\}$ 必发散
$\text{B.}$ 若 $\left\{x_n\right\}$ 收敛, 则 $\left\{y_n\right\}$ 必收敛
$\text{C.}$ 若 $\left\{\mathrm{x}_{\mathrm{n}}\right\}$ 有界,则 $\left\{\mathrm{y}_{\mathrm{n}}\right\}$ 必为无穷小
$\text{D.}$ 若 $\left\{\frac{1}{\mathrm{x}_{\mathrm{n}}}\right\}$ 有界,则 $\left\{\mathrm{y}_{\mathrm{n}}\right\}$ 必为无穷小
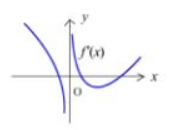
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续, 其导函数图形如图所示, 则 $f(x)$ 的极值点的个数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
关于函数 $y=x \ln x, x$ 定义域为 $(0,+\infty)$, 以下描述不正确的是
$\text{A.}$ 在区间 $\left(0, \mathrm{e}^{-1}\right)$ 单调递减
$\text{B.}$ 在 $\mathrm{x}=\mathrm{e}^{-1}$ 处取最小值
$\text{C.}$ $\left(e^{-1},-e^{-1}\right)$ 是曲线 $y=x \ln x$ 的拐点
$\text{D.}$ 曲线 $y=x \ln x$ 无渐近线
若函数 $f(x)=2^{\frac{1}{x}}+\arctan \frac{x|x|}{(x-1)(x-2)}$ 下面哪一条直线不是此函数的渐近线
$\text{A.}$ $x=0$
$\text{B.}$ $y=1-\frac{\pi}{4}$
$\text{C.}$ $x=2$
$\text{D.}$ $y=1+\frac{\pi}{4}$
$\lim _{x \rightarrow 0} \frac{\int_0^{x^2} \sin t^2 \mathrm{~d} t}{x^6}=$
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $1$