单选题 (共 3 题 ),每题只有一个选项正确
若 $f(x)=(x-1)^3+2(x-1)-\ln \frac{x}{2-x}+2$, 数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $S_1=\frac{1}{10}, 2 S_n=n a_{n+1}$, 则 $\sum_{i=1}^{19}\left[f\left(a_i\right)+f\left(a_{20-i}\right)\right]=$
$\text{A.}$ 76
$\text{B.}$ 38
$\text{C.}$ 19
$\text{D.}$ 0
若 $A$ 为函数 $f(x)=\mathrm{e}^x+x$ 图象上的一点, $B(2,0)$, 则 $|A B|$ 的最小值为
$\text{A.}$ $\sqrt{6}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $\frac{3 \sqrt{2}}{2}$
$\text{D.}$ 2
已知 $a, b, c$ 满足 $a=\log _5\left(2^b+3^b\right), c=\log _3\left(5^b-2^b\right)$, 则
$\text{A.}$ $|a-c| \geq|b-c|,|a-b| \geq|b-c|$
$\text{B.}$ $|a-c| \geq|b-c|,|a-b| \leq|b-c|$
$\text{C.}$ $|a-c| \leq|b-c|,|a-b| \geq|b-c|$
$\text{D.}$ $|a-c| \leq|b-c|,|a-b| \leq|b-c|$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\mathrm{e}^x-a x+b, a \in \mathbf{R}, b \in[-1,1]$.
(1) 当 $a=0$ 时, 求 $f(x)$ 在 $[0,+\infty)$ 上的值域;
(2) 当 $b=1$ 时, $\forall x \in(0,+\infty), f(x)>1$, 求 $a$ 的取值范围.
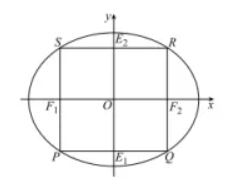
我们把各边与椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的对称轴垂直或平行的 $E$ 的内接四边形叫做 $E$ 的内接矩形. 如图, 已知四边形 $P Q R S$ 是 $E$ 的一个边长为 1 的内接正方形, $P S, Q R$ 分别与 $x$ 轴交于 $F_1, F_2$, 且 $F_1, F_2$ 为 $E$ 的两个焦点.
(1) 求 $E$ 的标准方程;
(2) 设 $A_i(i=1,2, \cdots, 100)$ 是四边形 $P Q R S$ 内部的 100 个不同的点, 线段 $P Q, R S$ 与 $y$ 轴分别交于 $E_1$, $E_2$, 记 $d_k=\sum_{i=1}^{100}\left|E_k A_i\right|$, 其中 $k=1,2$, 证明: $d_1, d_2$ 中至少有一个小于 $25(1+\sqrt{5})$.