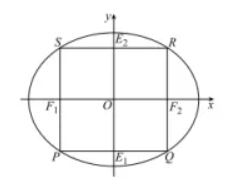
我们把各边与椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的对称轴垂直或平行的 $E$ 的内接四边形叫做 $E$ 的内接矩形. 如图, 已知四边形 $P Q R S$ 是 $E$ 的一个边长为 1 的内接正方形, $P S, Q R$ 分别与 $x$ 轴交于 $F_1, F_2$, 且 $F_1, F_2$ 为 $E$ 的两个焦点.
(1) 求 $E$ 的标准方程;
(2) 设 $A_i(i=1,2, \cdots, 100)$ 是四边形 $P Q R S$ 内部的 100 个不同的点, 线段 $P Q, R S$ 与 $y$ 轴分别交于 $E_1$, $E_2$, 记 $d_k=\sum_{i=1}^{100}\left|E_k A_i\right|$, 其中 $k=1,2$, 证明: $d_1, d_2$ 中至少有一个小于 $25(1+\sqrt{5})$.