一、解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
1. 在 中, 分别是角 、、 的对边, 且 .
(1) 求 ;
(2) 若 , 求 .
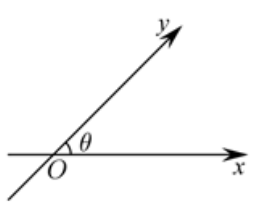
2. 数轴
的交点为
, 夹角为
, 与
轴、
轴正向同向的单位向量分别是
. 由平面向量基本定理, 对于平面内的任一向量
,存在唯一的有序实数对
, 使得
, 我们把
叫做点
在斜坐标系
中的坐标 (以下各点的坐标都指在斜坐标系
中的坐标).
(1) 若
为单位向量, 且
与
夹角为
, 求点
的坐标;
(2) 若
, 点
的坐标为
, 求向量
与
的夹角的余弦值.
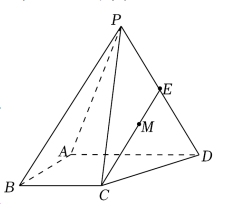
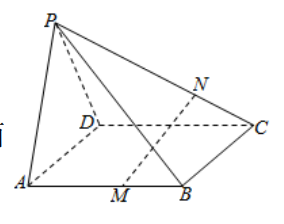
3. 如图所示, 在四棱椎
中,
平面
是
的中点.
(1) 求证:
;
(2) 若
是线段
上一动点, 则线段
上是否存在点
, 使
平面
? 说明理由.
4. 数学史上著名的波尔约 - 格维也纳定理:任意两个面积相等的多边形, 它们可以通过相互拼接得到. 它由法卡斯・波尔约 (FarksBolyai) 和保罗・格维也纳 (PaulGerwien) 两位数学家分别在 1833 年和 1835 年给出证明. 现在我们来尝试用平面图形拼接空间图形, 使它们的全面积都与原平面图形的面积相等: (1) 给出两块相同的正三角形纸片 (如图 1、图 2), 其中图 1, 沿正三角形三边中点连线折起, 可拼得一个正三棱椎; 图 2, 正三角形三个角上剪出三个相同的四边形 (阴影部分), 其较长的一组邻边边长为三角形边长的
, 有一组对角为直角, 余下部分按虚线折起, 可成一个缺上底的正三棱柱, 而剪出的三个相同的四边形恰好拼成这个正三棱椎的上底.
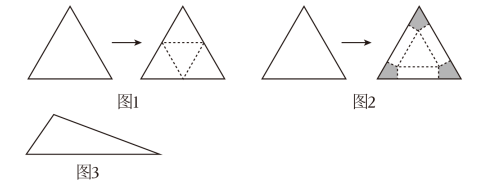
(1) 试比较图 1 与图 2 剪拼的正三棱椎与正三棱柱的体积的大小;
(2) 如果给出的是一块任意三角形的纸片 (如图 3), 要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等. 请仿照图 2 设计剪拼方案, 用虚线标示在图 3 中, 并作简要说明.
5. 已知复数 满足 , 且 的虚部为 在复平面内所对应的点在第四象限.
(1) 求 ;
(2) 若 在复平面上对应的点分别为 为坐标原点, .
6. 如图, 已知
是平行四边形
所在平面外一点,
、 分别是
、 的三等分点
靠近
靠近
;
(1) 求证:
平面
.
(2) 在
上确定一点
, 使平面
平面
.
7. 如图, 在
中,
为
中点,
为
上一点, 且满足
的面积为
,
(1) 求
的值;
(2) 求
的最小值.

8. 的内角 的对边分别为 , 且 .
(1) 求 ;
(2) 若 为 的外接圆上的点, , 求四边形 面积的最大值.
9. 如图, 已知四棱椎 的底面为菱形, 且 是棱 上的点, 是棱 的中点, 为四棱椎 的高, 且四面体 的体积为 .
(1) 证明: ;
(2) 若过点 的平面 与 平行, 且交 于点 , 求多面体 体积.
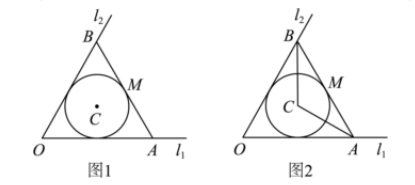
10. 如图 1,某景区是一个以 C 为圆心,半径为 3km 的圆形区域,道路 l1,l2 成 60° 角,且均和景区边界相切,现要修一条与景区相切的观光木栈道
,点
, 分别在
和
上,修建的木栈道
与道路
,围成三角地块
. (注:圆的切线长性质:圆外一点引圆的两条切线长相等).
(1) 当
为正三角形时求修建的木栈道
与道路
围成的三角地块
面积;
(2) 若
的面积
, 求木栈道
长;
(3) 如图 2, 设
,
①将木栈道
的长度表示为
的函数, 并指定定义域;
②求木栈道
的最小值.