数学史上著名的波尔约 - 格维也纳定理:任意两个面积相等的多边形, 它们可以通过相互拼接得到. 它由法卡斯・波尔约 (FarksBolyai) 和保罗・格维也纳 (PaulGerwien) 两位数学家分别在 1833 年和 1835 年给出证明. 现在我们来尝试用平面图形拼接空间图形, 使它们的全面积都与原平面图形的面积相等: (1) 给出两块相同的正三角形纸片 (如图 1、图 2), 其中图 1, 沿正三角形三边中点连线折起, 可拼得一个正三棱椎; 图 2, 正三角形三个角上剪出三个相同的四边形 (阴影部分), 其较长的一组邻边边长为三角形边长的 $\frac{1}{4}$, 有一组对角为直角, 余下部分按虚线折起, 可成一个缺上底的正三棱柱, 而剪出的三个相同的四边形恰好拼成这个正三棱椎的上底.
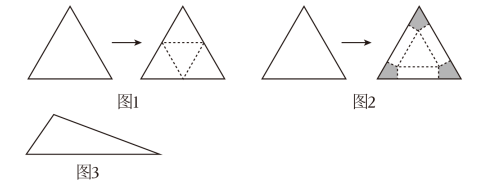
(1) 试比较图 1 与图 2 剪拼的正三棱椎与正三棱柱的体积的大小;
(2) 如果给出的是一块任意三角形的纸片 (如图 3), 要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等. 请仿照图 2 设计剪拼方案, 用虚线标示在图 3 中, 并作简要说明.

(1) 试比较图 1 与图 2 剪拼的正三棱椎与正三棱柱的体积的大小;
(2) 如果给出的是一块任意三角形的纸片 (如图 3), 要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等. 请仿照图 2 设计剪拼方案, 用虚线标示在图 3 中, 并作简要说明.