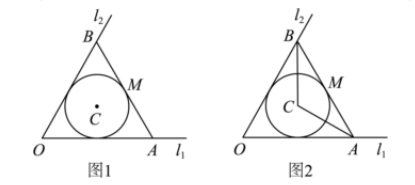
如图 1,某景区是一个以 C 为圆心,半径为 3km 的圆形区域,道路 l1,l2 成 60° 角,且均和景区边界相切,现要修一条与景区相切的观光木栈道 $AB$,点 $A,B$ 分别在 $l_1$和 $l_2$上,修建的木栈道 $AB$ 与道路$ l_1,l_2$围成三角地块 $OAB$. (注:圆的切线长性质:圆外一点引圆的两条切线长相等).
(1) 当 $\triangle O A B$ 为正三角形时求修建的木栈道 $A B$ 与道路 $l_1, l_2$ 围成的三角地块 $O A B$ 面积;
(2) 若 $\triangle O A B$ 的面积 $S=10 \sqrt{3}$, 求木栈道 $A B$ 长;
(3) 如图 2, 设 $\angle C A B=\alpha$,
①将木栈道 $A B$ 的长度表示为 $\alpha$ 的函数, 并指定定义域;
②求木栈道 $A B$ 的最小值.
(1) 当 $\triangle O A B$ 为正三角形时求修建的木栈道 $A B$ 与道路 $l_1, l_2$ 围成的三角地块 $O A B$ 面积;
(2) 若 $\triangle O A B$ 的面积 $S=10 \sqrt{3}$, 求木栈道 $A B$ 长;
(3) 如图 2, 设 $\angle C A B=\alpha$,
①将木栈道 $A B$ 的长度表示为 $\alpha$ 的函数, 并指定定义域;
②求木栈道 $A B$ 的最小值.
