单选题 (共 10 题 ),每题只有一个选项正确
在 $-1 , 0 , 1 ,-\frac{1}{3}$ 四个数中,最小的数是
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ $-\frac{1}{3}$
中央广播电视总台《2024年春节联欢晚会》以“龙行蠡蠡(da),欣欣家国”为主题,以“益”字为题眼,用“兢兢”之姿生动描摹1400000000中华儿女奋发有为、昂扬向上的精神风貌. 其中数字 1400000000 用科学记数法表示为
$\text{A.}$ $1.4 \times 10^8$
$\text{B.}$ $1.4 \times 10^9$
$\text{C.}$ $14 \times 10^8$
$\text{D.}$ $0.14 \times 10^{10}$
中国传统文化博大精深.下面四个图形其中既是轴对称图形又是中心对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
某校5位同学在“国学经典诵读”比赛中,成绩 (单位: 分) 分别是 $86 , 95 , 97 , 90 , 88$. 这组数据的中位数是
$\text{A.}$ 86
$\text{B.}$ 88
$\text{C.}$ 90
$\text{D.}$ 95
下列多边形中,内角和最大的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
要使分式 $\frac{2-x}{x-1}$ 有意义, $x$ 的取值范围满足
$\text{A.}$ $x \neq 1$
$\text{B.}$ $x \neq 0$
$\text{C.}$ $x \neq 2$
$\text{D.}$ $x \neq-1$
下列运算结果正确的是
$\text{A.}$ $x^3 \cdot x^4=x^{12}$
$\text{B.}$ $\left(-2 x^2\right)^3=-8 x^6$
$\text{C.}$ $x^6 \div x^3=x^2$
$\text{D.}$ $x^2+x^3=x^5$
若关于 $x$ 的一元二次方程 $x^2+x+m=0$ 有两个相等的实数根,则实数 $m$ 的值为
$\text{A.}$ -4
$\text{B.}$ $-\frac{1}{4}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ 4
如图,点 $A 、 B 、 C$ 在 $\odot O$ 上, $\angle O B C=18^{\circ}$ ,则 $\angle A=$
$\text{A.}$ $18^{\circ}$
$\text{B.}$ $36^{\circ}$
$\text{C.}$ $72^{\circ}$
$\text{D.}$ $144^{\circ}$
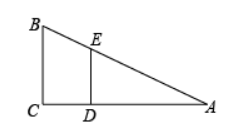
如图,某班上体育课,甲、乙两名同学分别站在 $C 、 D$ 的位置时,乙的影子 $D A$ 恰好与甲影子 $C A$ 在同一条直线上,已知甲身高 1.8 米,乙身高 1.5 米,甲的影长是 6 米,则甲、乙两同学相距()米.
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 5
填空题 (共 6 题 ),请把答案直接填写在答题纸上
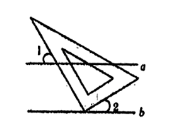
如图,直角三角板的直角顶点放在直线 $b$ 上,且 $ a // b , \angle 1=55^{\circ} $ 则 $ \angle 2 $ 的度数为
若反比例函数 $\mathrm{y}=\frac{k}{x}$ 的图象经过点(1, - 6),则 $\mathrm{k}$ 的值为
方程组 $\left\{\begin{array}{l}x-y=1 \\ 3 x+y=7\end{array}\right.$ 的解为
扇形的圆心角为 $120^{\circ}$ ,半径为 4 ,则扇形的面积为
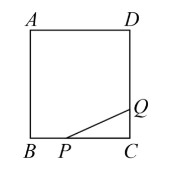
如图,在正方形 $A B C D$ 中, $A B=6, P, Q$ 分别为 $B C, C D$ 上一点,且 $B P=C Q$ ,连接 $P Q$ ,则 $P Q$ 的最小值是
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式组: $\left\{\begin{array}{c}x>\frac{x+2}{3} \\ 5 x-3 < 5+x\end{array}\right.$.
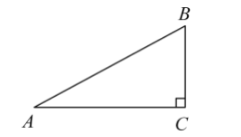
如图,在Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, A B=6$.
(1) 根据要求用尺规作图:作 $\angle C A B$ 的平分线交 $B C$ 于点 $D$; (不写作法,只保留作图痕迹. )
(2) 在 (1) 的条件下, $C D=1$ ,求 $\triangle A D B$ 的面积.
先化简,再求值: $\frac{a}{a^2+2 a+1} \div\left(1-\frac{1}{a+1}\right)$ 其中 $a=\sqrt{3}-1$
在“乡村振兴”工作中,某养殖场加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,2021年10月份和12月份的产蛋量分别是4万千克与4.84万千克,求养殖场这两个月蛋鸡产蛋量的月平均增长率.
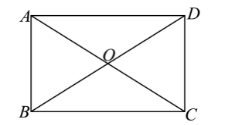
如图, $\square A B C D$ 的对角线 $A C 、 B D$ 相交于点 $O , \triangle O A B$ 是等边三角形, $A B=4$.
(1)证明 $\square A B C D$ 是矩形;
(2)求 $\square A B C D$ 的面积.
2022年4月15日是第七个全民国家安全教育日.为增强师生的国家安全意识,我区某中学组织了“国家安全知识竞赛”,根据学生的成绩划分为A、B、C、D四个等级,根据图中提供的信息,回答下列问题
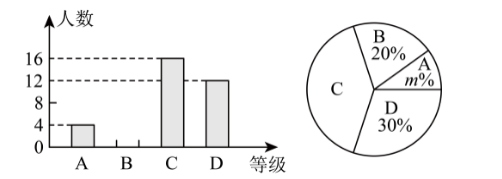
(1)参加知识竞赛的学生共有
(2)扇形统计图中, $m=$ , $C$ 等级对应的圆心角为 $\qquad$度;
(3)小永是四名获 $A$ 等级的学生中的一位,学校将从获 $A$ 等级的学生中任选 2 人,参加区举办的知识竞赛,求小永被选中参加区知识竞赛的概率.
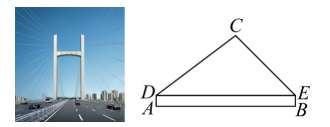
郑北大桥横跨亚洲最大铁路编组站,该桥为独塔双索面钢混结合梁斜拉桥,是国内同类型桥中桥面最宽的结合梁斜拉桥. 某数学“综合与实践”小组的同学把“测量郑北大桥的某组斜拉索最高点到桥面的距离作为一项课题活动,进行了探究,具体过程如下:
【方案设计】 如图,分别在 $A, B$ 两点放置测角仪,测得 $\angle C D E$ 和 $\angle C E D$ 的度数,并量出 $A B$ 的距离,即可解决问题:
【数据收集】 $\angle C D E=37^{\circ}, \angle C E D=45^{\circ}, A B=347$ 米,测角仪 $A D$ 和 $B E$ 的高度为 1.5 米;
【问题解决】求郑北大桥某组斜拉索最高点 $C$ 到桥面 $A B$ 的距离. (结果保留整数. 参考数据: $\sin 37^{\circ} \approx 0.6, \cos 37^{\circ} \approx 0.8, \tan 37^{\circ} \approx 0.75$ )
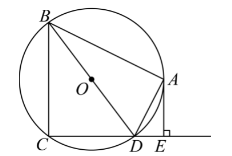
如图,四边形 $\mathrm{ABCD}$ 内接于 $\odot \mathrm{O}, \mathrm{BD}$ 是 $\odot \mathrm{O}$ 的直径, $\mathrm{AE} \perp \mathrm{CD}$ 于点 $\mathrm{E}, \mathrm{DA}$ 平分 $\angle \mathrm{BDE}$.
(1) 求证: $\mathrm{AE}$ 是 $\odot \mathrm{O}$ 的切线;
(2) 如果 $\mathrm{AB}=4 , \mathrm{AE}=2$ ,求 $\odot \mathrm{O}$ 的半径.
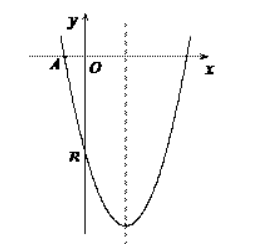
如图,已知二次函数 $y=a x^2-4 x+c$ 的图象与坐标轴交于点 $A(-1,0)$ 和点 $B(0,-5)$.
(1) 求该二次函数的解析式;
(2) 已知该函数图象的对称轴上存在一点 $P$ ,使得 $\triangle A B P$ 的周长最小. 请求出点 $P$ 的坐标.