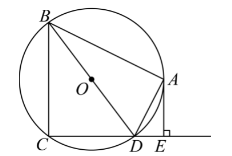
如图,四边形 $\mathrm{ABCD}$ 内接于 $\odot \mathrm{O}, \mathrm{BD}$ 是 $\odot \mathrm{O}$ 的直径, $\mathrm{AE} \perp \mathrm{CD}$ 于点 $\mathrm{E}, \mathrm{DA}$ 平分 $\angle \mathrm{BDE}$.
(1) 求证: $\mathrm{AE}$ 是 $\odot \mathrm{O}$ 的切线;
(2) 如果 $\mathrm{AB}=4 , \mathrm{AE}=2$ ,求 $\odot \mathrm{O}$ 的半径.
(1) 求证: $\mathrm{AE}$ 是 $\odot \mathrm{O}$ 的切线;
(2) 如果 $\mathrm{AB}=4 , \mathrm{AE}=2$ ,求 $\odot \mathrm{O}$ 的半径.
