下列判断正确的是

下列四个运算中, 只有一个是正确的. 这个正确运算的序号是
(1) $3^0+3^{-1}=-3$;
(2) $\sqrt{5}-\sqrt{2}=\sqrt{3}$;
(3) $\left(2 a^2\right)^3=8 a^5$;
(4) $-a^8 \div a^4=-a^4$.

如图1, 将一个边长为 $m$ 的正方形纸片剪去两个小长方形得到一个如图 2 所示的图形, 再将剪下的两个小长方形拼成如图 3 所示的一个新的长方形, 则图 3 中的长方形的周长为

如图, 在菱形 $A B C D$ 中, $A B=B D$, 点 $E 、 F$ 分别在 $B C 、 C D$ 上, 且 $B E=C F$, 连接 $B F 、 D E$交于点 $M$, 延长 $E D$ 到 $H$ 使 $D H=B M$, 连接 $A M, A H$, 则以下四个结论:
(1) $\triangle B D F \cong \triangle D C E$;
(2) $\angle B M D=120^{\circ}$;
(3) $\triangle A M H$ 是等边三角形;
(4) $S_{\text {四边形 } A B M D}=\frac{\sqrt{3}}{4} A M^2$.
其中正确结论的个数是

如图, 圆环中大圆的半径为 $r$, 小圆的半径为 $\frac{r}{2}, A B$ 为大圆的直径, 则阴影部分的面积为

如图, 在直角坐标系的第一象限内, $\triangle A O B$ 是边长为 2 的等边三角形, 设直线 $l: x=t(0 \leq t \leq 2)$ 截这个三角形所得位于直线左侧的图形 (阴影部分) 的面积为 $s$, 则 $s$ 关于 $t$ 的大致图象是

在一个不透明的袋子里装有 2 个红球和 1 个白球, 它们除颜色外都相同, 从中摸出一个球, 放回搅匀后, 再摸出一个球。两次都摸到红球的概率是

如图, $\odot O, \odot O_1$ 都经过 $A 、 B$ 两点, 且点 $O$ 在 $\odot O_1$ 上, 连接 $A O$ 并延长,交 $\odot O$ 于点 $C$, 连接 $B C$ 交 $\odot O_1$ 于点 $D$, 连接 $A D, A D \perp B O$, 若 $A B=3$, 则 $\overparen{B D}$ 的长为

小强用一根长为 $16 \mathrm{~cm}$ 的铁丝围成矩形, 则矩形的最大面积是

在 $\frac{1}{2}, 0,-1,-\frac{1}{2}$ 这四个数中, 最小的数是

若 $4 x^2+m x+n=(a x+2)^2$, 则 $m= , a= , n= $.

若 $a+\frac{1}{a}=\sqrt{11}$, 则 $a-\frac{1}{a}$ 的值为

如图, 点 $C$ 在线段 $A B$ 上, 且 $A C=2 B C$, 分别以 $A C 、 B C$ 为边在线段 $A B$ 的同侧作正方形 $A C$ $D E 、 B C F G$, 连接 $E C 、 E G$, 则 $\tan \angle C E G=$

若 $|a-2|+\sqrt{b+3}+(c-4)^2=0$, 则 $a-b-c=$.

如图, 一块含 $30^{\circ}$ 角的直角三角板 $A B C, B C=1$, 应该是将其绕点 $A$ 顺时针旋转得到 $A B^{\prime} C^{\prime}$, 当 $B, A, C^{\prime}$ 在一条直线上时, 顶点 $C$ 所走的路径长为

如图, 在 $\square A B C D$ 中, $G$ 是 $C D$ 上一点, 连接 $B G$ 且延长交 $A D$ 的延长线于点 ${ }^A$ $E, A F=C G, \angle E=30^{\circ}, \angle C=50^{\circ}$, 则 $\angle B F D=$.

解方程 $3(x-1)=(x-1)^2$.

如图, 已知: Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $D$ 是 $B C$ 的中点, 点 $P$ 是 $B C$ 边上的一个动点.
(1) 如图 1, 若点 $P$ 与点 $D$ 重合, 连接 $A P$, 则 $A P$ 与 $B C$ 的位置关系是
(2) 如图 2, 若点 $P$ 在线段 $B D$ 上, 过点 $B$ 作 $B E \perp A P$ 于点 $E$, 过点 $C$ 作 $C F \perp A P$ 于点 $F$, 则 $C F, B E$ 和 $E F$ 这三条线段之间的数量关系是
(3) 如图3, 在 ( 2 ) 的条件下, 若 $B E$ 的延长线交直线 $A D$ 于点 $M$, 求证: $C P=A M$ ；
(4) 如图 4 , 已知 $B C=4$, 若点 $P$ 从点 $B$ 出发沿着 $B C$ 向点 $C$ 运动, 过点 $B$ 作 $B E \perp A P$ 于点 $E$, 过点 $C$ 作 $C F \perp A P$ 于点 $F$, 设线段 $B E$ 的长度为 $d_1$, 线段 $C F$ 的长度为 $d_2$, 试求出点 $P$ 在运动的过程中 $d_1+d_2$ 的最大值.

如图, 已知同一平面内四个点 $A, B, C, D$, 请按要求完成下列问题:
(1) 画直线 $A B$, 射线 $B D$, 连接 $A C$;
(2) 在线段 $A C$ 上求作点 $P$, 使得 $C P=A C-A B$ ； ( 保留作图痕迹 )
( 3 ) 过点 $P$ 作直线 $l$, 使得 $l / / A B$; ( 保留作图痕迹)
(4) 请在直线 $l$ 上确定一点 $Q$, 使点 $Q$ 到点 $C$ 与点 $D$ 的距离之和最短, 并写出画图的依据.

阅读下列两则材料, 回答问题
材料一: 我们将 $(\sqrt{a}+\sqrt{b})$ 与 $(\sqrt{a}-\sqrt{b})$ 称为一对“对偶式”
因为 $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=(\sqrt{a})^2-(\sqrt{b})^2=a-b$, 所以构造“对偶式”相乘可以有效地将 $(\sqrt{a}+$ $\sqrt{b})$ 和 $(\sqrt{a}-\sqrt{b})$ 中的“ $\sqrt{ }$ ”去掉

例如: 已知 $\sqrt{25-x}-\sqrt{15-x}=2$, 求 $\sqrt{25-x}+\sqrt{15-x}$ 的值.
解: $(\sqrt{25-x}-\sqrt{15-x}) \times(\sqrt{25-x}+\sqrt{15-x})=(25-x)-(15-x)=10$
$$
\begin{aligned}
& \because \sqrt{25-x}-\sqrt{15-x}=2, \\
& \therefore \sqrt{25-x}+\sqrt{15-x}=5
\end{aligned}
$$

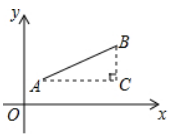
材料二: 如图, 点 $A\left(x_1, y_1\right)$, 点 $B\left(x_2, y_2\right)$, 以 $A B$ 为斜边作Rt $\triangle A B C$,
则 $C\left(x_2, y_1\right)$, 于是 $A C=\left|x_1-x_2\right|, B C=\left|y_1-y_2\right|$, 所以
$$
A B=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \text {. }
$$

反之, 可将代数式 $\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}$ 的值看作点 $\left(x_1, y_1\right)$ 到点 $\left(x_2, y_2\right)$ 的距离. 例如
$$
\sqrt{x^2-2 x+y^2+2 y+2}=\sqrt{\left(x^2-2 x+1\right)+\left(y^2+2 y+1\right)}=\sqrt{(x-1)^2+(y+1)^2}=\sqrt{(x-1)^2+[y-(-1)]^2} .
$$

所以可将代数式 $\sqrt{x^2-2 x+y^2+2 y+2}$ 的值看作点 $(x, y)$ 到点 $(1,-1)$ 的距离.
(1) 利用材料一, 解关于 $x$ 的方程: $\sqrt{20-x}-\sqrt{4-x}=2$, 其中 $x \leq 4$ ；
(2)①利用材料二, 求代数式 $\sqrt{x^2-2 x+y^2-16 y+65}+\sqrt{x^2+4 x+y^2-4 y+8}$ 的最小值, 并求出此时 $y$ 与 $x$ 的函数关系式, 写出 $x$ 的取值范围;
② 将①所得的 $y$ 与 $x$ 的函数关系式和 $x$ 的取值范围代入 $y=\sqrt{2 x^2+5 x+12}+\sqrt{2 x^2+3 x+6}$ 中解出 $x$, 直接写出 $x$ 的值.

如图, 已知直线 $y=2 x+2$ 与抛物线 $y=a x^2+b x+c$ 相交于 $A, B$ 两点, 点 $A$ 在 $x$ 轴上, 点 $B$ 在 $y$ 轴上, 点 $C(3,0)$ 在抛物线上.
(1) 求该抛物线的表达式；
(2) 正方形 $O P D E$ 的顶点 $O$ 为直角坐标系原点, 顶点 $P$ 在线段 $O C$ 上, 顶点 $E$ 在 $y$ 轴正半轴上, 若 $\triangle A O B$ 与 $\triangle D P C$ 全等, 求点 $P$ 的坐标;
(3) 在条件 (2) 下, 点 $Q$ 是线段 $C D$ 上的动点 (点 $Q$ 不与点 $D$ 重合), 将 $\triangle P O D$ 沿 $P Q$ 所在的直线翻折得到 $\triangle P O D^{\prime}$, 连接 $A D^{\prime}$, 求 $A D^{\prime}$ 长度的取值范围.