单选题 (共 10 题 ),每题只有一个选项正确
下列实数是无理数的是( )
$\text{A.}$ $-2$
$\text{B.}$ $\frac{1}{6}$
$\text{C.}$ $\sqrt{9}$
$\text{D.}$ $\sqrt{11}$
若 $\alpha=70^{\circ}$, 则 $\alpha$ 的补角的度数是 ( )
$\text{A.}$ $130^{\circ}$
$\text{B.}$ $110^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $20^{\circ}$
若一个正方形的面积是 12 , 则它的边长是( )
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ 3
$\text{C.}$ $3 \sqrt{2}$
$\text{D.}$ 4
下列几何体中,其俯视图与主视图完全相同的是 ( )
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列各式中计算结果为 $x^{6}$ 的是 ( )
$\text{A.}$ $x^{2}+x^{4}$
$\text{B.}$ $x^{8}-x^{2}$
$\text{C.}$ $x^{2} \cdot x^{4}$
$\text{D.}$ $x^{12} \div x^{2}$
生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为 ( )

$\text{A.}$ 1.24米
$\text{B.}$ 1.38米
$\text{C.}$ 1.42米
$\text{D.}$ 1.62米
已知 $x=1$ 是一元二次方程 $(m-2) x^{2}+4 x-m^{2}=0$ 的一个根, 则 $m$ 的值为 ( )
$\text{A.}$ - 1 或 2
$\text{B.}$ $-1$
$\text{C.}$ 2
$\text{D.}$ 0
如图所示的木制活动衣帽架是由三个全等的菱形构成, 根据实际需 要可以调节 $A E$ 间的距离. 若 $A E$ 间的距离调节到 $60 \mathrm{~cm}$, 菱形的边长 $A B=20 \mathrm{~cm}$, 则 $\angle D A B$ 的度数是 ( )
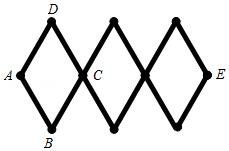
$\text{A.}$ $90^{\circ}$
$\text{B.}$ $100^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $150^{\circ}$
如图, $A$ 是 $\odot O$ 上一点, $B C$ 是直径, $A C=2, A B=4$, 点 $D$ 在 $\odot O$ 上且平分 $\widehat{B C}$, 则 $D C$ 的 长为 ( )
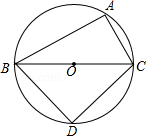
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $2 \sqrt{5}$
$\text{D.}$ $\sqrt{10}$
如图(1), 正方形 $A B C D$ 中, $A C, B D$ 相交于点 $O, E$ 是 $O D$ 的中点. 动点 $P$ 从点 $E$ 出发, 沿着 $E \rightarrow O \rightarrow B \rightarrow A$ 的路径以每秒 1 个单位长度的速度运动到点 $A$, 在此过程中线段 $A P$ 的 长度 $y$ 随着运动时间 $x$ 的函数关系如图(2)所示, 则 $A B$ 的长为

$\text{A.}$ $4 \sqrt{2}$
$\text{B.}$ 4
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $2 \sqrt{2}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
如果盈利 100 元记作 $+100$ 元, 那么兮损 50 元记作 ( ) 元.
暑假期间,亮视眼镜店开展学生配镜优惠活动.某款式眼镜的广告如下,请你为广告牌填上原价.

要使分式 $\frac{x+2}{x-1}$ 有意义, $x$ 需满足的条件是
在一个不透明的袋中装有若干个材质、大小完全相同的红球, 小明在袋中放入 3 个黑球(每 个黑球除颜色外其余都与红球相同), 摇匀后每次随机从袋中摸出一个球, 记录颜色后放 回袋中, 通过大量重复摸球试验后发现, 摸到红球的频率稳定在 $0.85$ 左右, 估计袋中红 球有 ( ) 个.
如图, 在平面直角坐标系中, $\triangle O A B$ 的顶点 $A, B$ 的坐标分别为 $(3, \sqrt{3}),(4,0)$. 把 $\triangle O A B$ 沿 $x$ 轴向右平移得到 $\triangle C D E$, 如果点 $D$ 的坐标为 $(6, \sqrt{3})$, 则点 $E$ 的坐标为

若一个扇形的圆心角为 $60^{\circ}$, 面积为 $\frac{\pi}{6} \mathrm{~cm}^{2}$, 则这个扇形的弧长为 ( ) (结果保留 $\pi$ ).
已知 $y=\sqrt{(x-4)^{2}}-x+5$, 当 $x$ 分别取 $1,2,3, \cdots, 2020$ 时, 所对应 $y$ 值的总和是
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(2-\sqrt{3})(2+\sqrt{3})+\tan 60^{\circ}-(\pi-2 \sqrt{3}) ^0$.
解不等式组: $\left\{\begin{array}{l}3 x-5 < x+1 \\ 2(2 x-1) \geq 3 x-4\end{array}\right.$ ,并把它的解集在数轴上表示出来.

如图, 在 $\triangle A B C$ 中, $D$ 是 $B C$ 边上一点, 且 $B D=B A$.
(1) 尺规作图 (保留作图痕迹, 不写作法):
(1) 作 $\angle A B C$ 的角平分线交 $A D$ 于点 $E$;
(2)作线段 $D C$ 的垂直平分线交 $D C$ 于点 $F$.
(2) 连接 $E F$, 直接写出线段 $E F$ 和 $A C$ 的数量关系及位置关系.

图(1)是甘肃省博物馆的镇馆之宝 - - 铜奔马, 又称 “马踏飞燕”, 于 1969 年 10 月出土于武 威市的雷台汉墓, 1983 年 10 月被国家旅游局确定为中国旅游标志. 在很多旅游城市的广 场上都有 “马踏飞燕” 雕塑. 某学习小组把测量本城市广场的 “马踏飞燕” 雕塑 (图(2)) 最高点离地面的高度作为一次课题活动, 同学们制定了测量方案, 并完成了实地测量, 测得结果如下表:

请你根据上表中的测量数据, 帮助该小组求出 “马踏飞燕”雕塑最高点离地面的高度(结 果保留一位小数). (参考数据: $\sin 31^{\circ} \approx 0.52, \cos 31^{\circ} \approx 0.86, \tan 31^{\circ} \approx 0.60, \sin 42^{\circ}$ $\approx 0.67, \cos 42^{\circ} \approx 0.74, \tan 42^{\circ} \approx 0.90$ )

2019 年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一. 截至 2020 年 1 月,
甘肃省已有五家国家 $5 A$ 级旅游景区, 分别为 $A$ : 嘉峪关文物景区; $B$ : 平凉崆峒山风景
名胜区; $C$ : 天水麦积山景区; $D$ : 敦煌鸣沙山月牙泉景区; $E$ : 张掖七彩丹霞景区. 张 帆同学与父母计划在暑假期间从中选择部分景区游玩.
(1) 张帆一家选择 $E$ : 张掖七彩丹霞景区的概率是多少?
(2)若张帆一家选择了 $E$ : 张掖七彩丹霞景区, 他们再从 $A, B, C, D$ 四个景区中任选 两个景区去旅游, 求选择 $A, D$ 两个景区的概率(要求画树状图或列表求概率).
习近平总书记于2019年8月在兰州考察时说“黄河之滨也很美”.兰州是古丝绸之路商贸重镇,也是黄河唯一穿城而过的省会城市,被称为“黄河之都”.近年来,在市政府的积极治理下,兰州的空气质量得到极大改善,“兰州蓝”成为兰州市民引以为豪的城市名片.如图是根据兰州市环境保护局公布的2013~2019年各年的全年空气质量优良天数绘制的折线统计图.

请结合统计图解答下列问题:
(1) 2019 年比 2013 年的全年空气质量优良天数增加了多少天;
(2) 这七年的全年空气质量优良天数的中位数是;
(3)求这七年的全年空气质量优良天数的平均天数;
(4)《兰州市 “十三五” 质量发展规划》中指出: 2020 年, 确保兰州市全年空气质量优 良天数比率达 $80 \%$ 以上. 试计算 2020 年(共 366 天)兰州市空气质量优良天数至少需要 多少天才能达标.
通过课本上对函数的学习,我们积累了一定的经验.下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:

(1)当 $x=$ 时, $y=1.5$;
(2)根据表中数值描点 $(x, y)$, 并画出函数图象;
(3)观察画出的图象, 写出这个函数的一条性质:

如图, $\odot O$ 是 $\triangle A B C$ 的外接圆, 其切线 $A E$ 与直径 $B D$ 的延长线相交于点 $E$, 且 $A E=A B$.
(1) 求 $\angle A C B$ 的度数;
(2) 若 $D E=2$, 求 $\odot O$ 的半径.

如图, 点 $M, N$ 分别在正方形 $A B C D$ 的边 $B C, C D$ 上, 且 $\angle M A N=45^{\circ}$. 把 $\triangle A D N$ 绕点 $A$ 顺时针旋转 $90^{\circ}$ 得到 $\triangle A B E$.
(1) 求证: $\triangle A E M \cong \triangle A N M$.
(2) 若 $B M=3, D N=2$, 求正方形 $A B C D$ 的边长.

如图, 在平面直角坐标系中, 抛物线 $y=a x^{2}+b x-2$ 交 $x$ 轴于 $A, B$ 两点, 交 $y$ 轴于点 $C$, 且 $O A=2 O C=8 O B$. 点 $P$ 是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2) 若 $P C / / A B$, 求点 $P$ 的坐标;
(3) 连接 $A C$, 求 $\triangle P A C$ 面积的最大值及此时点 $P$ 的坐标.
