一、单选题 (共 8 题 ),每题只有一个选项正确
1. 在平面直角坐标系 中, 已知点 , 则点 关于 轴的对称点的坐标是
2. 数学中有许多精美的曲线, 以下是 “笛卡尔叶形线” “阿基米德螺线” “三叶玫瑰线” 和 “星形 线". 其中一定不是轴对称图形的是
3. 地球是人与自然共同生存的家园, 在这个家园中, 还住着许多常常被人们忽略的微小生命. 在 冰岛海岸的黄铁矿粘液池中的古菌身上, 科学家发现了基因片段, 并提取出了最小的生命体, 它的直径仅为 米. 将数字 用科学记数法表示为
4. 在下列运算中, 正确的是
5. 下列式子从左到右变形正确的是
6. 将一副直角三角板按如图所示的位置摆放, 若
, 则图中
的 度数是

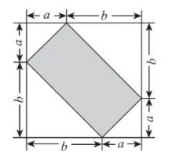
7. 如图, 四个等腰直角三角形拼成一个正方形, 则阴影部分的面积为
8. 对于分式 为常数 , 若当 时, 该分式总有意义; 当 时, 该分式的值为负数. 则 与 0 的大小关系正确的是
二、填空题 (共 6 题 ),请把答案直接填写在答题纸上
10. 如果等腰三角形的两边长分别是 和 , 则该等腰三角形周长是
11. 当 时, 分式 的值为 0 .
12. 如图, 点
在正五边形的边
上运动 (不与点
重合), 若
, 则
的取值范围是

13. 如图, 在 中, , 点 分别在边 上, 若沿直线 折叠, 点 恰好与点 重合, 且 , 则 ,
14. 甲乙两位同学进行一种数学游戏. 游戏规则是:两人轮流对
及
对应的边或角 添加等量条件 (点
分别是点
的对应点). 某轮添加条件后, 若能判定
与
全等, 则当轮添加条件者失败, 另一人获胜.

上表记录了两人游戏的部分过程, 则下列说法正确的是 (塤写所有正 确结论的序号 ).
(1) 若第 3 轮甲添加
, 则乙获胜;
(2) 若甲想获胜, 第 3 轮可以添加条件
;
(3) 若乙想获胜, 可修改第 2 轮添加条件为
.
三、解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
15. 计算: .
17. 化简: .
18. 如图, 两车从路段
的两端同时出发, 沿平行路线以相同的速度行驶, 相同时间后分别到 达
两地.
两地到路段
的距离相等吗? 为什么?

19. 已知 , 求代数式 的值.
20. 如图, 已知线段
与直线
平行.
(1) 作
的角平分线
交直线
于点
( 尺规作图, 保留作图痕迹, 不写作法);
(2) 在 (1) 的条件下, 若
的中点为
, 连接
并延长交直线
于点
, 请用等式表 示线段
之间的数量关系:

21. 随着科技的发展,人工智能使生产生活更加便捷高效. 某科技公司生产了一批新型搬运机器 人, 打出了如下的宣传:

根据该宣传, 求新型机器人每天搬运的货物量.
22. 我们知道, 代数式的运算和多项式因式分解都属于不改变代数式值的恒等变形. 探究下列关 于 的代数式, 并解决问题.
(1) 若计算 的结果为 , 则
(2) 若多项式 分解因式的结果为 , 则
(3) 若计算 的结果为 , 求 的值.
23. 在平面直角坐标系
中, 横、纵坐标都是整数的点叫做整点. 如图, 点
的坐标分 别为
.
(1)
(2) 若点
为整点, 且满足
, 直接写出点
的坐标 (写出两个即可).

24. 已知 .
(1) 若 , 求 的值;
(2) 在 (1) 的条件下, 且 为整数, 求 的值.
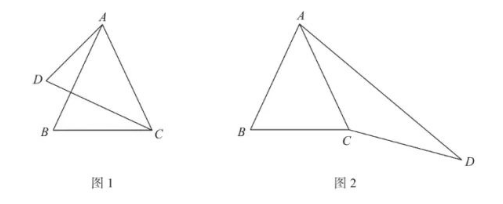
25. 已知在
中,
, 且
. 作
, 使得
.
(1) 如图 1, 若
与
互余, 则
(用含
的代数式表示 );
(2) 如图 2, 若
与
互补, 过点
作
于点
, 求证:
;
(3) 若
与
的面积相等, 则
与
满足什么关系? 请直接写出你的结论.
26. 在平面直角坐标系
中, 点
分别在线段
上, 如果存在点
使得
且
(点
逆时针排列), 则称点
是线段
的 “关联点” . 如图 1, 点
是线段
的 “关联点”。
(1) 如图 2, 已知点
, 点
与点
重合.
① 当点
是线段
中点时, 在
中, 其中是线段
的 “关联点” 的是
② 已知点
是线段
的 “关联点”, 则点
的坐标是

(2) 如图 3, 已知
.
①当点
与点
重合, 点
在线段
上运动时 (点
不与点
重合), 若点
是线 段
的 “关联点”, 求证:
;
②当点
分別在线段
上运动时, 直接写出线段
的 “关联点”
形成的 区域的周长.
