单选题 (共 3 题 ),每题只有一个选项正确
如图,在矩形 $A B C D$ 中无重叠放入面积分别为 $16 \mathrm{~cm}^2$ 和 $12 \mathrm{~cm}^2$ 的两张正方形纸片,则图中空白部分的面积为
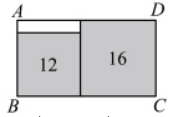
$\text{A.}$ $(8-4 \sqrt{3}) \mathrm{cm}^2$
$\text{B.}$ $(4-2 \sqrt{3}) \mathrm{cm}^2$
$\text{C.}$ $(16-8 \sqrt{3}) \mathrm{cm}^2$
$\text{D.}$ $(8 \sqrt{3}-12) \mathrm{cm}^2$
定义: 如果两个分式的积等于这两个分式的差乘以一个常数,那么这两个分式叫做和谐分式. 如 $\frac{1}{n+1} \times \frac{1}{n+3}=\frac{1}{2}\left(\frac{1}{n+1}-\frac{1}{n+3}\right)$ ,则 $\frac{1}{n+1}$ 与 $\frac{1}{n+3}$ 是和谐分式. 下列每组两个分式是和谐分式的是
$\text{A.}$ $\frac{1}{n}$ 与 $\frac{1}{2 n+1}$
$\text{B.}$ $\frac{1}{2 n-1}$ 与 $\frac{1}{3 n+1}$
$\text{C.}$ $\frac{2}{2 n-1}$ 与 $\frac{3}{3 n+1}$
$\text{D.}$ $\frac{3}{2 n-1}$ 与 $\frac{2}{3 n+1}$
如图,从等边三角形内一点 $P$ 向三边作垂线,垂足分别是 $Q 、 R 、 S 、 P Q=3 , P R=4 , P S=5$ ,则 $\triangle A B C$ 的面积是
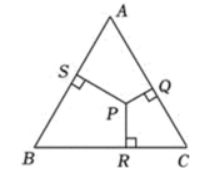
$\text{A.}$ $48$
$\text{B.}$ $48 \sqrt{3}$
$\text{C.}$ $96$
$\text{D.}$ $96 \sqrt{3}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
已知实数 $m 、 n$ 在数轴上的对应点如图所示,化简 $\sqrt{m^2}-\sqrt{(m-n)^2}-|m+n|=$

解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
对于平面直角坐标系 $x O y$ 中的点 $P(a, b)$ ,若点 $P^{\prime}$ 的坐标为 $\left(a+\frac{b}{k}, k a+b\right)$ (其中 $k$ 为常数,且 $k \neq 0$ ),则称点 $P^{\prime}$ 为点 $P$ 的“ $k$ 之称心点”. 例如: $P(1,4)$的“ 2 之称心点”为 $P^{\prime}\left(1+\frac{4}{2}, 2 \times 1+4\right)$ , 即 $P^{\prime}(3,6)$.
(1)①点 $P(-1,-2)$ 的“ 2 之称心点” $P$ 的坐标为
②若点 $P$ 的“ $k$ 之称心点” $P^{\prime}$ 的坐标为 $(3,3)$ ,请写出一个符合条件的点 $P$ 的坐标
(2)若点 $P$ 在 $y$ 轴的正半轴上,点 $P$ 的“ $k$ 之称心点”为 $P^{\prime}$ 点,且 $\triangle O P P^{\prime}$ 为等腰直角三角形,则 $k$ 的值为
(3)在 (2) 的条件下,若关于 $\mathrm{x}$ 的分式方程 $\frac{2 x+5}{x-3}+\frac{2-m x}{3-x}=k$ 无解,求 $\mathrm{m}$ 的值.