解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
袋中有 2 个白球, 3 个红球, 5 个黄球,这 10 个小球除颜色外完全相同.
(1)从袋中任取 3 个球,求恰好取到 2 个黄球的概率;
(2)从袋中任取 2 个球,记取到红球的个数为 $\xi$ ,求 $\xi$ 的分布列、期望 $E(\xi)$ 和方差 $D(\xi)$ .
甲、乙两名同学与同一台智能机器人进行象棋比赛,计分规则如下:在一轮比赛中,如果甲赢而乙输,则甲得 1 分;如果甲输而乙赢,则甲得 -1 分;如果甲和乙同时赢或同时输,则甲得 0 分.设甲赢机器人的概率为 0.7 ,乙赢机器人的概率为 0.6 .求:
(1)在一轮比赛中,甲的得分 $\xi$ 的分布列;
(2)在两轮比赛中,甲的得分 $\eta$ 的期望和方差。
某公司计划在 2023 年年初将 200 万元用于投资,现有两个项目供选择.项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利 $30 \%$ ,也可能亏损 $15 \%$ ,且这两种情况发生的概率分别为 $\frac{7}{9}$ 和 $\frac{2}{9}$ ;项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利 $50 \%$ ,可能损失 $30 \%$ ,也可能不赔不赚,且这三种情况发生的概率分别为 $\frac{3}{5}, \frac{1}{3}, \frac{1}{15}$ .
(1)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(2)若市场预期不变,该投资公司按照(1)中选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润 + 本金)可以翻两番?(参考数据 $\lg 2 \approx 0.3010, \lg 3 \approx 0.4771$ )
某高校“植物营养学专业”学生将鸡冠花的株高增量作为研究对象,观察长效肥和缓释肥对农作物影响情况.其中长效肥、缓释肥、未施肥三种处理下的鸡冠花分别对应1,2,3三组.观察一段时间后,分别从1,2,3三组随机抽取40株鸡冠花作为样本,得到相应的株高增量数据整理如下表.
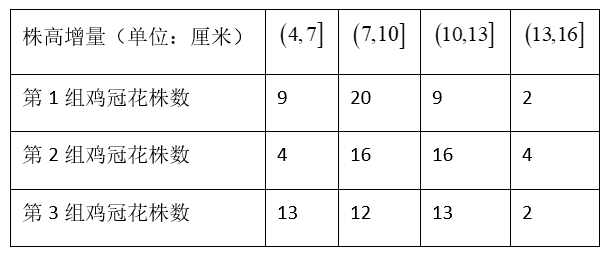
假设用频率估计概率,且所有鸡冠花生长情况相互独立.
(1)从第1组所有鸡冠花中随机选取1株,估计株高增量为 $(7,10]$ 厘米的概率;
(2)分别从第1组,第2组,第3组的所有鸡冠花中各随机选取1株,记这 3 株鸡冠花中恰有 $X$ 株的株高增量为 $(7,10]$ 厘米,求 $X$ 的分布列和数学期望 $E X$ ;
(3)用"$\xi_k=1$"表示第 $k$ 组鸡冠花的株高增量为 $(4,10], ~ " \xi_k=0$"表示第 $k$ 组鸡冠花的株高增量为 $(10,16]$ 厘米, $k=1,2,3$ ,直接写出方差 $D \xi_1, D \xi_2, D \xi_3$ 的大小关系.(结论不要求证明)
甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得 10 分,负方得 0 分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军,已知甲学校在三个项目中获胜的概率分别为 $0.5,0.4,0.8$ ,各项目的比赛结果相互独立.
(1)求甲学校获得冠军的概率;
(2)用 $X$ 表示乙学校的总得分,求 $X$ 的分布列与期望.
(3)设用 $Y$ 表示甲学校的总得分,比较 $D X$ 和 $D Y$ 的大小(直接写出结果).
某公司为活跃气氛提升士气,年终拟通过抓阄兑奖的方式对所有员工进行奖励.规定:每位员工从一个装有4个标有面值的阄的袋中一次性随机摸出2个阄,阄上所标的面值之和为该员工获得的奖励金额.
(1)若袋中所装的4个阄中有1个所标的面值为800元,其余3个均为200元,求
①员工所获得的奖励为1000元的概率;
②员工所获得的奖励额的分布列及数学期望;
(2)公司对奖励额的预算是人均1000元,并规定袋中的4个阄只能由标有面值200元和800元的两种阄或标有面值400元和600元的两种阄组成.为了使员工得到的奖励总额尽可能符合公司的预算且每位员工所获得的奖励额相对均衡,请对袋中的4个阄的面值给出一个合适的设计,并说明理由.
为迎接 2022 年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动。该滑雪场的收费标准是:滑雪时间不超过 1 小时免费,超过 1 小时的部分每小时收费标准为 40 元(不足 1 小时的部分按 1 小时计算)。有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过 1 小时离开的概率分别为 $\frac{1}{4}, \frac{1}{6} ; 1$ 小时以上且不超过 2小时离开的概率分别为 $\frac{1}{2}, \frac{2}{3}$ ;两人滑雪时间都不会超过 3 小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量 $\xi$ ,求 $\xi$ 的分布列与均值 $E(\xi)$ ,方差 $D(\xi)$ .