单选题 (共 23 题 ),每题只有一个选项正确
袋中装有红球 3 个、白球 2 个、黑球 1 个,从中任取 2 个,则互斥而不对立的两个事件是
$\text{A.}$ 至少有一个白球;都是白球
$\text{B.}$ 至少有一个白球;至少有一个红球
$\text{C.}$ 至少有一个白球;红、黑球各一个
$\text{D.}$ 恰有一个白球;一个白球一个黑球
将四位数 2023 的各个数字打乱顺序重新排列,则所组成的不同的四位数(含原来的四位数)中两个 2 不相邻的概率为
$\text{A.}$ $\frac{5}{9}$
$\text{B.}$ $\frac{5}{24}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{2}{3}$
银行储蓄卡的密码由 6 位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后 1 位数字,如果记得密码的最后 1 位是偶数,不超过 2 次就按对的概率是
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{1}{3}$
我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是"每个大于 2 的偶数可以表示为两个素数的和",如 $40=3+37$ .在不超过 40 的素数中,随机选取两个不同的数,其和等于 40 的概率是
$\text{A.}$ $\frac{1}{12}$
$\text{B.}$ $\frac{1}{14}$
$\text{C.}$ $\frac{1}{22}$
$\text{D.}$ $\frac{1}{24}$
从 $5,7,9,11,13$ 中随机取 2 个不同的数,则这 2 个数之和是 4 与 6 的公倍数的概率是
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{1}{10}$
$\text{D.}$ $\frac{3}{10}$
某同学口袋中共有 5 个大小相同、质地均匀的小球•其中 3 个编号为 5,2 个编号为 10 ,现从中取出 3 个小球,编号之和恰为 20 的概率为
$\text{A.}$ $\frac{1}{15}$
$\text{B.}$ $\frac{4}{15}$
$\text{C.}$ $\frac{8}{15}$
$\text{D.}$ $\frac{3}{5}$
三位同学参加某项体育测试,每人要从 100 m 跑、引体向上、跳远、铅球四个项目中选出两个项目参加测试,则有且仅有两人选择的项目完全相同的概率是
$\text{A.}$ $\frac{1}{12}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{5}{12}$
$\text{D.}$ $\frac{7}{12}$
下列有关事件的说法正确的是
$\text{A.}$ 若 $P(A \cup B)=P(A)+P(B)=1$ ,则事件 $A, B$ 为对立事件
$\text{B.}$ 事件 $A, B$ 中至少有一个发生的概率一定比 $A, B$ 中恰有一个发生的概率大
$\text{C.}$ 若 $A, B$ 为互斥事件,则 $P(A)+P(B) \leq 1$
$\text{D.}$ 若事件 $A, B, C$ 满足条件 $P(A)>0, B$ 和 $C$ 为互斥事件,则 $P((B \cup C) \mid A)>P(B \mid A)+P(C \mid A)$
教育部为发展贫困地区教育,在全国部分大学培养教育专业公费师范生,毕业后分配到相应的地区任教。现将 5 名男大学生, 4 名女大学生平均分配到甲、乙、丙 3 所学校去任教,则
$\text{A.}$ 甲学校没有女大学生的概率为 $\frac{5}{21}$
$\text{B.}$ 甲学校至少有两名女大学生的概率为 $\frac{25}{42}$
$\text{C.}$ 每所学校都有男大学生的概率为 $\frac{6}{7}$
$\text{D.}$ 乙学校分配 2 名女大学生, 1 名男大学生且丙学校有女大学生的概率为 $\frac{1}{7}$
由 1,2,3,4,5组成的没有重复数字的五位数,从中任意抽取一个,则其恰好为"前 3 个数字保持递减,后 3 个数字保持递增"(如五位数" 43125 ",前 3 个数字" 431 "保持递减,后 3 个数字" 125 "保持递增)的概率是( )
$\text{A.}$ $\frac{1}{20}$
$\text{B.}$ $\frac{1}{12}$
$\text{C.}$ $\frac{1}{10}$
$\text{D.}$ $\frac{1}{6}$
4 位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为
$\text{A.}$ $\frac{1}{8}$
$\text{B.}$ $\frac{3}{8}$
$\text{C.}$ $\frac{5}{8}$
$\text{D.}$ $\frac{7}{8}$
在集合 $\{1,2,3,4,5\}$ 中任取一个偶数 $a$ 和一个奇数 $b$ 构成以原点为起点的向量 $a=(a, b)$ .从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为 $n$ ,其中面积不超过 4 的平行四边形的个数为 $m$ ,则 $\frac{m}{n}=$
$\text{A.}$ $\frac{4}{15}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{2}{3}$
某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为 $p_1, p_2, p_3$ ,且 $p_3>p_2>p_1>0$ 。记该棋手连胜两盘的概率为 $p$ ,则
$\text{A.}$ $p$ 与该棋手和甲、乙、丙的比赛次序无关
$\text{B.}$ 该棋手在第二盘与甲比赛,$p$ 最大
$\text{C.}$ 该棋手在第二盘与乙比赛,$p$ 最大
$\text{D.}$ 该棋手在第二盘与丙比赛,$p$ 最大
将一颗质地均匀的骰子(各面上分别标有点数 $1,2,3,4,5,6$ )先后抛掷 3 次,至少出现 1 次 6 点向上的概率是( )。
$\text{A.}$ $\frac{5}{216}$
$\text{B.}$ $\frac{25}{216}$
$\text{C.}$ $\frac{31}{216}$
$\text{D.}$ $\frac{91}{216}$
投掷一枚均匀硬币和一枚均匀骰子各一次,记"硬币正面向上"为事件 A ,"骰子向上的点数是 $3^{\prime \prime}$ 为事件 B ,则事件 A , B 中至少有一件发生的概率是
$\text{A.}$ $\frac{5}{12}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{7}{12}$
$\text{D.}$ $\frac{3}{4}$
如图中有一个信号源和五个接收器.接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号.若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所得六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
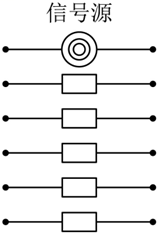
$\text{A.}$ $\frac{4}{45}$
$\text{B.}$ $\frac{1}{36}$
$\text{C.}$ $\frac{4}{15}$
$\text{D.}$ $\frac{8}{15}$
从编号为 $1,2, \ldots, 10$ 的 10 个大小相同的球中任取 4 个,则所取 4 个球的最大号码是 6 的概率为( )
$\text{A.}$ $\frac{1}{84}$
$\text{B.}$ $\frac{1}{21}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{3}{5}$
将 $1,2, \ldots, 9$ 这 9 个数平均分成三组,则每组的三个数都成等差数列的概率为( )
$\text{A.}$ $\frac{1}{420}$
$\text{B.}$ $\frac{1}{336}$
$\text{C.}$ $\frac{1}{70}$
$\text{D.}$ $\frac{1}{56}$
甲、乙两人独立地解同一问题,甲解决这个问题的概率是 $p_1$ ,乙解决这个问题的概率是 $p_2$ ,那么恰好有 1 人解决这个问题的概率是
$\text{A.}$ $p_1 p_2$
$\text{B.}$ $p_1\left(1-p_2\right)+p_2\left(1-p_1\right)$
$\text{C.}$ $1-p_1 p_2$
$\text{D.}$ $1-\left(1-p_1\right)\left(1-p_2\right)$
从 5 张 100 元, 3 张 200 元, 2 张 300 元的奥运预赛门票中任取 3 张,则所取 3 张中至少有 2 张价格相同的概率为 .
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{79}{120}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{23}{24}$
生物实验室有 5 只兔子,其中只有 3 只测量过某项指标,若从这 5 只兔子中随机取出 3 只,则恰有 2 只测量过该指标的概率为
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{1}{5}$
甲、乙、丙三位同窗打算利用假期外出游览,约定每人从泰山、孔府这两处景点中任选一处,那么甲、乙两位同学恰好选取同一处景点的概率是
$\text{A.}$ $\frac{2}{9}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{2}$
从 $1,2,3,4$ 中任取 2 个不同的数,则取出的 2 个数之差的绝对值为 2 的概率是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{6}$
多选题 (共 2 题 ),每题有多个选项正确
某个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,设 $M=$"该家庭中有男孩、又有女孩",$N=$"该家庭中最多有一个女孩",则下列结论正确的是()
$\text{A.}$ 若该家庭中有两个小孩,则 $M$ 与 $N$ 互斥
$\text{B.}$ 若该家庭中有两个小孩,则 $M$ 与 $N$ 不相互独立
$\text{C.}$ 若该家庭中有三个小孩,则 $M$ 与 $N$ 不互斥
$\text{D.}$ 若该家庭中有三个小孩,则 $M$ 与 $N$ 相互独立
$A, B$ 为随机事件,已知 $P(A)=0.5, P(B)=0.3$ ,下列结论中正确的是( )
$\text{A.}$ 若 $A, B$ 为互斥事件,则 $P(A+B)=0.8$
$\text{B.}$ 若 $A, B$ 为互斥事件,则 $P(\bar{A}+\bar{B})=0.8$
$\text{C.}$ 若 $A, B$ 是相互独立事件,$P(A+B)=0.65$
$\text{D.}$ 若 $P(B \mid A)=0.5$ ,则 $P(B \mid \bar{A})=0.1$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知甲、乙、丙、丁四位高三学生拍毕业照,这四位同学排在同一行,则甲、乙两位学生相邻的概率为
从甲、乙等 5 名同学中随机选 3 名参加社区服务工作,则甲、乙至少一人入选的概率为
某商场举行抽奖活动,箱子里有 10 个大小一样的小球,其中红色的 5 个,黄色的 3 个,蓝色的 2 个,现从中任意取出 3 个,则其中至少含有两种不同颜色的小球的概率为 $\_\_\_\_$。