单选题 (共 4 题 ),每题只有一个选项正确
已知直线 $I_1:(3-a) x+y-1=0$ 和 $Z_2: a x+(4 a-10) y+3=0$ ,则"$a=2$"是"直线 $I_1$ 与直线 $Z_2$ 垂直"的( )
$\text{A.}$ 充分非必要条件
$\text{B.}$ 必要非充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既非充分也非必要条件
$l, m, n$ 为直线,$\alpha, \beta, \gamma$ 为平面,则下列命题中为真命题的是
$\text{A.}$ 若 $m / / \alpha, n / / \beta, m / / n$ ,则 $\alpha / / \beta$
$\text{B.}$ 则 $m \perp \alpha, n \perp \alpha$ ,则 $m / / n$
$\text{C.}$ 若 $\alpha \perp \gamma, \beta \perp \gamma$ ,则 $\alpha \perp \beta$
$\text{D.}$ 则 $\alpha \perp \beta, I \subseteq \alpha$ ,则 $I \perp \beta$
对于一个古典概型的样本空间 $\Omega$ 和事件 A、B、C、D,其中 $n(\Omega)=60, n(A)=30, n(B)=10$ , $n(C)=20, n(D)=30, n(A \cup B)=40, n(A \cap C)=10, n(A \cup D)=60$ ,则 $(\quad)($ 注:$n(A)$表示集合 A 的元素个数)
$\text{A.}$ A 与 $B$ 不互斥
$\text{B.}$ A 与 $D$ 互斥但不对立
$\text{C.}$ $C$ 与 $D$ 互斥
$\text{D.}$ A 与 $C$ 相互独立
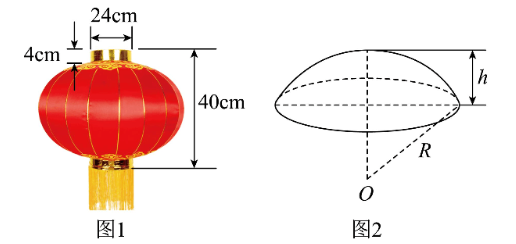
灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一第种喜庆的氛围.如图 1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球面的一部分(除去两个球缺).如图 2 ,"球缺"是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为 $V=\frac{\pi}{3}(3 R-h) h^2$ ,其中 $R$ 是球的半径,$h$ 是球缺的高.已知该灯笼的高为 40 cm ,圆柱的高为 4 cm ,圆柱的底面圆直径为 24 cm ,则该灯笼的体积为(取 $\pi=3$ )
$\text{A.}$ $33664 \mathrm{~cm}^3$
$\text{B.}$ $33792 \mathrm{~cm}^3$
$\text{C.}$ $34674 \mathrm{~cm}^3$
$\text{D.}$ $35456 \mathrm{~cm}^3$
填空题 (共 12 题 ),请把答案直接填写在答题纸上
已知一个球的表面积为 $36 \pi$ ,则该球的半径为
若圆锥的底面半径为 3 ,母线长为 5 ,则圆锥的侧面积是
若圆 $C_1: x^2+y^2=1$ 与圆 $C_2:(x-3)^2+(y-4)^2=k+26$ 外切,则实数 $k=$
已知空间向量 $\vec{a}=(1,2,3), \vec{b}=(2,-2,0), \vec{c}=(1,1, \lambda)$ ,若 $\vec{c} \perp(2 \vec{a}+b)$ ,则 $\lambda=$
某小组成员的年龄分布茎叶图如图所示,则该小组成员年龄的第 25 百分位数是

在正四面体 $A B C D$ 中,直线 $B C$ 与 $A D$ 所成角的大小为
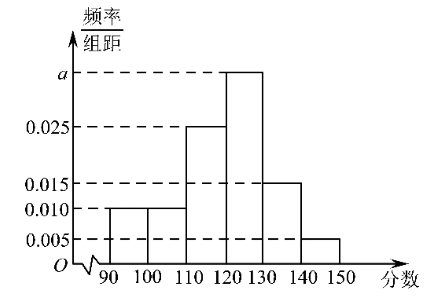
8.某校共有 400 名学生参加了趣味知识竞赛(满分: 150 分),且每位学生的竞赛成续均不低于 90 分.将这 400 名学生的竞赛成绩分组如下:$[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]$ ,得到的频率分布直方图如图所示,则这 400 名学生中竟赛成绩不低于 120 分的人数为
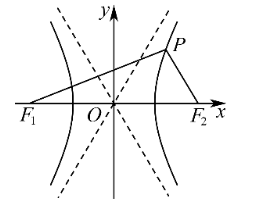
已知双曲线 $x^2-\frac{y^2}{3}=1$ 的左、右焦点分别为 $F_1 、 F_2$ ,双曲线上的点 $P$ 在第一象限,且 $P F_2$ 与双曲线的一条渐近线平行,则 $\triangle P F_1 F_2$ 的面积为 .
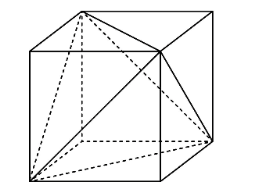
如图,求一个棱长为 $\sqrt{2}$ 的正四面体的体积,可以看成一个棱长为 1 的正方体截去四个角后得到,类比这种方法,一个三对棱长相等的四面体 $A B C D$ ,其三对棱长分别为 $A B=C D=\sqrt{5}, A D=B C=\sqrt{13}, A C=B D=\sqrt{10}$ ,则此四面体的体积为
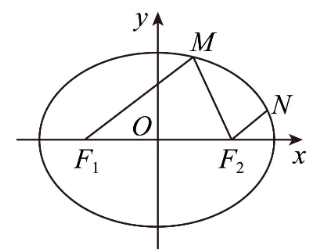
如图,已知 $F_1, F_2$ 分别是椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点,$M, N$ 为椭圆上两点,满足 $F_1 M / / F_2 N$ ,且 $\left|F_2 N\right|:\left|F_2 M\right|:\left|F_1 M\right|=1: 2: 3$ ,则椭圆 $C$ 的离心率为
已知空间向量 $\vec{a} 、 \vec{b} 、 \vec{c}$ 满足:$|\vec{a}|=|\vec{b}|=4,|\vec{c}|=1$ ,若 $|\vec{c}-\vec{a}| \cdot(\vec{c}-\vec{b})=0$ ,则 $|\vec{a}-\vec{b}|^2$ 的取值范围为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知抛物线 $C: y^2=4 x$ 的焦点为 $F$ .
(1)求抛物线 $C$ 的焦点坐标和准线方程;
(2)过焦点 $F$ 的直线 $l$ 与抛物线交于 $\mathrm{A} 、 B$ 两点,若 $|A F|=3$ ,求线段 $B$ 的长.
如图,已知在四棱柱 $A B C D-E F G H$ 中,$E A \perp$ 平面 $A B C D, N 、 M$ 分别是 $E F 、 H D$ 的中点.
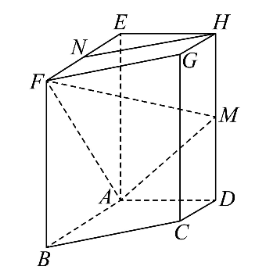
(1)求证:$H N / /$ 平面 $A F M$ ;
(2)若底面 $A B C D$ 为梯形,$A B / / C D, A B=E A=2, A D=D C=1$ ,异面直线 $A B$ 与 $E H$ 所成角为 $\frac{\pi}{2}$ ,求三棱锥 $N-A F M$ 的体积.
A 校高一年级共有学生 330 名,为了解该校高一年级学生的身高情况,学校采用分层随机抽样的方法抽取 66 名学生,其中女生 32 名,男生 34 名,测量他们的身高。
(1)该校高一学生中男、女生各有多少名?
(2)在 32 名女生身高的数据中,其中一个数据记录有误,错将 165 cm 记录为 156 cm ,由错误数据求得这 32 个数据的平均数为 161 cm ,方差为 23.6875 ,求原始数据的平均数及方差(平均数结果保留精确值,方差结果精确到 0.01 ).
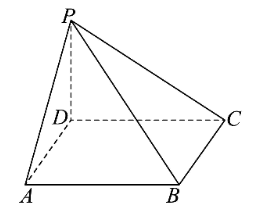
如图,在四棱锥 $P-A B C D$ 中,底面 $A B C D$ 为正方形,$P D \perp$ 底面 $A B C D, P D=A B=4$ ,且 $\overrightarrow{P M}=\lambda \overrightarrow{P B},(\lambda \in[0,1])$.
(1)求证:$P B \perp A C$ ;
(2)当 $\angle A M C$ 为针角时,求实数 $\lambda$ 的取值范围;
(3)若二面角 $M-A C-B$ 的大小为 $45^{\circ}$ ,求点 $P$ 到平面 $A M C$ 的距离.
已知椭圆 $\frac{x^2}{8}+\frac{y^2}{4}=1$ 的左、右焦点分别为 $F_1 、 F_2$ ,过坐标原点的直线交椭圆于 $A 、 B$ 两点,点 $A$ 在第一象限.
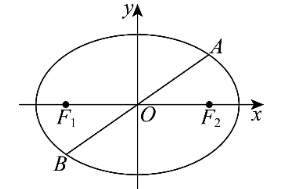
(1)若 $|O A|=\sqrt{6}$ ,求点 $A$ 的坐标;
(2)求 $\left|\overrightarrow{A F_1}+3 \overrightarrow{A F_2}\right|$ 的取值范围;
(3)若 $A E \perp x$ 轴,垂足为 $E$ ,连结 $B E$ 并延长交椭圆于点 $C$ ,求 $\triangle A B C$ 面积的最大值.